Kulcsmondat: sorbarendezünk, különböző elemeket és minden elemet felhasználunk
Az összes esetet általában az elemek sorbarendezési lehetőségeinek a száma adja, amely \(n\) elem esetén \(n!=1\cdot 2\cdot\ldots\cdot n\). A nehezebb kérdés a "kedvező" esetek számának meghatározása szokott lenni, amelynek összeszámolásában egyes elemek rögzítése, elemek csoportjának külön sorbarendezése vagy komplementer esemény alapján történő összeszámolás segíthet.
A példa alapján értelmezzük a fenti definíciók közül az eseményt és azok szorzatát, függetlenségét. Legyen az \(M\) esemény az, hogy a hat betűból az első három helyen az \(A,B,C\) betűk állnak valamilyen sorrendben. Az \(N\) esemény pedig legyen, az hogy a hat betűből álló sorozat utolsó három betűje \(D,E,F\) valamilyen sorrendben. A két esemény szorzata \((M\cdot N)\) azt jelenti, hogy hat betűt sorba rendezünk úgy, hogy az első három az \(A,B,C\) betűk valamilyn sorrendben ÉS az utolsó három betű a \(D,E,F\) valamilyen sorrendben. A betűk nem keveredhetnek, azaz az első három helyen nem lehet \(D,E,F\) betűk egyike sem, amely azt jelenti, hogy ha az első három pozíciót feltöltöttük az \(A,B,C\) betűkkel, akkor az utolsó három helyre már adódik, hogy mely betűk kerülhetnek, azaz a két esemény nem független.
Ha jobban belegondolunk, akkor \(M\), \(N\) és \((M\cdot N)\) események ugyanazt jelentik, csak más megfogalmazásban.
Kulcsmondat: sorbarendezünk, különböző elemeket és NEM minden elemet használunk fel
Sok hasonlóság van a permutáció és a variáció között, ugyanis mindkét esetben különböző elemek sorrendjéről beszélünk. A lényeges eltérés, hogy nem minden rendelkezésre álló elemet használunk fel. Ha szeretnénk megérteni az alapvető különbséget, akkor gondoljuk végig, hogy mindkét esetben a sor elejére \(n\) elem közül választunk, majd másodikra \((n-1)\) féle elem elemből és így tovább. Ezt a sort a permutáció esetén addig folytatjuk, amíg minden elem el nem fogy, míg a variációnál előbb megállunk pl. a \(k\). elemnél.
A feladat alapján gondoljuk át a kizáró események definícióját. Az első feladatunk, hogy a matematikai logikában tanult tagadást megfelelően alkalmazzuk, a kizáró esemény megfogalmazására, azaz \(10\) emberből \(3\)-at választunk ki, akiket véletlenszerűen sorbarendezünk és a második helyen nem Péter áll. Ezalatt azt értjük, hogy lehet, hogy a kiválasztott emberek között nincs is Péter, illetve ha kiválasztottuk, akkor nem álhat a második helyen. A kizáró esemény megfogalmazásából is látszik, hogy ha ezt a feladatot kellene megoldanunk, akkor két esetet is meg kellene vizsgálni: (1) amikor kiválasztottuk Pétert, és (2) amikor nem választottuk be az első \(3\) sorbaállítandó ember közé.
A valószínűségszámítás során is jól használható a kedvező események összeszámlálásakor a komplementer-esemény, így ha a fentiekben megfogalmazott kizáró esemény szerint kellene a sorbarendezést elkészíteni és az adott feltételeknek megfelelő sorrendek valószínűségét meghatározni, akkor érdemes az összes lehetőséget tartalmazó esemény számából kivonni azt amikor Péter a második helye áll.
Kulcsmondat: kiválasztunk, különböző elemeket és a kiválasztás sorrendje nem számít
Amennyiben a különböző elemekből választunk ki néhányat úgy, hogy a kiválasztás sorrendje nem számít, akkor kombinációról beszélünk. A feladatból is látszik, hogy a sorrendiség benne lehet a feladatban, de a megoldás során mégsem a sorbarendezésen alapuló eljárásokat alkalmazzuk.
Fogalmazzuk át a feladatok úgy, hogy annak tartalma ne változzon, de ne szerepeljen benne a sorbarendezésre utaló rész. \(1\)-től \(10\)-ig felírjuk az egész számokat egy-egy papírlapra, majd váletlenszerűen 10 ember húz belőle. Mennyi a valószínűsége, hogy az \(1\)-es és a \(2\)-es számot is éppen a két barátunk húzta? (mindegy, hogy melyik barátunk melyiket húzza.)
Az átfogalmazott feladatból látszik, hogy nem számít, hogy melyik barátunk melyik számot húzta, csak az, hogy \(1\)-es vagy \(2\)-es legyen, azaz csak egyetlen jó lehetőség van, ha a sorrendtől eltekintünk. Az összes lehetőség tetszőleges két kártya kihúzását jelenti, a sorrendre való tekintet nélkül, amely \(\dbinom{10}{2}\) féleképpen lehetséges.
Természetesen permutációval is megoldható a feladat. Az első helyre a két barátunk közül egyet választunk, a másodikra pedig a másik kerül. Ezt \(2\cdot 1\) féleképpen tehetjük meg. A többi helyre, hasonlóan gondolkodva \(8!\) féleképpen rendezhetjük el az embereket. Az összes lehetőség \(10\) elem összes sorrendje, azaz \(10!\), így a keresett valószínűség:
Kulcsmondat: sorbarendezünk, NEM FELTÉTLENÜL különböző elemeket és minden elemet felhasználunk
Azoknál a feladatoknál, ahol azonos elemek is szerepelhetnek a sorbarendezésben az ismétléses permutációt használhatjuk. Az azonos elemek nem minden feladatban jelentenek ténylegesen azonos elemeket, csak azt szeretnénk érzékeltetni, hogy azok sorrendje nem számít. A feladatok megoldása során azokat az elemeket, amelyek sorrendje nem számít egy pillanatra különbözőnek tekintjük, kiszámítjuk az összes lehetséges sorrendet, amely azonos az ismétlés nélküli permutációval, majd az így kapott eredményt elosztuk az azonos elemek egymás közi lehetséges sorrendjeinek számával. Ez az osztás még nem a valószínűség meghatározásához szükséges, ez az összes lehetőség kiszámításának a módja, azaz a nevezőt határozzuk meg a klasszikus valószínűségi modellben.
A példában lényegében \(8\) próbababa sorredjét kell meghatároznunk, amely csak kétféle (férfi és női) ahhoz, hogy a kedvező esetek számát megkapuk, ugyanis a két gyerek próbababát kiemelhetjük és a \(8\) maradék bábu sorbarendezését követően a két szélére állíthatjuk őket. Az utolsó lépés nem jelent többlet lehetőséget, ugyanis a két gyerekbábu sorrendje nem számít, így ez csak egyetlen módon végezhető el.
Kulcsmondat: sorbarendezünk, NEM FELTÉTLENÜL különböző elemeket és NEM minden elemet használunk fel
Érdemes átgondolni, hogy az ismétléses permutációba és variációban mit is jelent az ismétléses szó. A permutáció esetén az ismétlés arra vonatkozik, hogy meghatározott számú azonos elem van, azaz ezek ismétlődnek a sorbarendezés során. A célunk ezzel, hogy az ismétlődő elemek sorrendjét figyelmen kívül hagyjuk. Az ismétléses variációban minden elem különböző, de amikor válsztunk belőlük, akkor minden esetben a teljes skálából választhatunk, olyan, mintha minden estben visszatennénk a választható elemek közé az éppen kiválasztottat.
Fontos, hogy a fentiekben modellezett visszatevés nem azonos a visszatevéses mintavétellel, amelyet a következő oldalakon tárgyalunk.
Kulcsmondat: az egyes alapesemények bekövetkezésének valószínűsége minden esetben azonos, a mintavétel egyes lépései függetlenek egymástól és pontosan egy \(k\) értékre vonatkozó valószínűséget keresünk
Az általános képlethez három lépésben juthatunk el, amely \(n\) elemből pontosan \(k\) darab adott tulajdonságú elem kiválasztását jelenti, úgy hogy a kiválasztott elemet visszatesszük, azaz minden kiválasztás független a többitól. \(p\) annak a valószínűsége, hogy a kiválasztott elem rendelkezik az adott tulajdonsággal. A mellékelt példa tartalmazza a számszerű levezetést, amely három lépésből áll, az altalános képlet pedig a következő alakban írható fel. A három lépés: (1) \(n\) elemől kiválasztunk \(k\) darabot; (2) a \(k\) elem előfordulási valószínűsége \(p^k\); (3) a maradék \(n-k\) elem előfordulási valószínűsége \((1-p)^{n-k}\)
A \(P(X=k)\) jelölés azt a valószínűséget jelöli, amikor az \(X\) valószínűségi változó értéke pontosan \(k\), azaz \(n\) elemű mintában pontosan \(k\) elem rendelkezik a kívánt tulajdonsággal.
Kulcsmondat: az egyes alapesemények bekövetkezésének valószínűsége minden esetben azonos, a mintavétel egyes lépései függetlenek egymástól és legfeljebb \(k\) értékre vonatkozó valószínűséget keresünk
Az általános képlet az előző részben találhatóból származtatható, ugyanis a legfeljebb \(k\) azt jelenti, hogy pontosan \(0,1,2,\ldots k\) értékekre kell meghatározni a valószínűségeket. Az események kizárják egymást így a \(P(A+B)=P(A)+P(B)\) összefüggés használható.
A visszatevés nélküli mintavétel természetesebbenk tűnik, mint a visszatevés nélküli, ugyanis ebben azesetben nem fordulhat elő, hogy egy elemet többször is kiválasztunk. Ennek a mintavételi eljárásnak a matematikai tulajdonságai azonba sokkal kedvezőtlenebbek, mint a visszatevésesé. Az egyes mintavételek nem függetlenek egymástól, azaz ezek nem független események, valószínűségszámítási szempontból. További hátránya, hogy az egyes mintavételekkor az adott tulajdonságú elem kiválasztásának valószínűsége nem állandó.
A felső keretes részben leírt visszatevés nélküli modell jelöléseit használva az összes lehetőséget könnyen meghatározhatjuk, \(N\) elemből választunk \(n\)-et, ameleyt \(\dbinom{N}{n}\) féleképpen tehetünk meg. Ez lesz a keresett valószínűség nevezője.
A számláló meghatározásához gondolatban osszuk két csoportra az \(N\) elemet, az egyik csoportba tegyük a "selejteket", amelyek száma \(s\), a másikba pedig a "hibátlanokat", amelyek száma \((N-s)\). Ha \(n\) darabot választunk ki és azt szeretnénk, hogy pontosan \(k\) selejt legyen benne, akkor a selejtek csoportjából \(\dbinom{s}{k}\) féleképpen választhatunk selejtet és \(\dbinom{N-s}{n-k}\) féleképpen választhatunk "hibátlant". Az általános képlet:
Természetesen, ha arra vagyunk kíváncsik, hogy legfeljebb \(k\) elem rendelkezik az adott tulajdonsággal ("selejt"), akkor a visszatevéses modellhez hasonlóan itt is összegezhetjük \(X=1,2,\ldots,k\) esetekre a fenti valószínűséget.
Speciális esetként, visszatevés nélküli mintavételkor lehet az a feladatunk, hogy a kiválasztott elemek számával kapcsolatban az az elvárás, hogy mindegyik kedvező tulajdonságú legyen, azaz \(k=0\). A korábbi képletből látszik, hogy ebben az esetben a számlálóban szereplő első, \(\dbinom{s}{k}\) tag 1, ugyanis \(k=0\). A számláló így nem más, mint annak a száma, hogy a hibátlanokból hányféleképpen tudunk \(k\) darabot választani.
Ha helyesen meg tudjuk határozni a feladat típusát, akkor a képletet a függvénytáblázatból is kikereshetjük. A visszatevéses modellre vonatkozó képlet a Binomiális eloszlás címszónál található meg.
Az általános képlet értelmezése alapján az tkeressük, hogy mennyi a\(P(k\leq 1)\) értéke, azaz a selejtek száma \(0\) vagy \(1\). A \(k=0\) esetet az első tag jelöli, amely nevezőjében az összes lehetőség szerepel, azaz \(40\) forrasztásból \(4\)-et választunk ki. Mivel \(k=0\), így az \(s=6\) selejtből \(0\) választunk ki, az \(N-s=40-6\) hibátlan forrasztásból pedig \(n-k=4-0=4\)-et. A számlálóban ezek szorzata található.
\(k=1\) esetre hasonlóan vezethetjük végig a képlet felírását, amelyet az előzőhöz hozzá kell adnunk, a keretes részben lévő, kizáró eseményekre vonatkozó megállapítás alapján.
A logikai levezetést most mellőzzük, ugyanis a képlet általános levezetésénél már áttekintettük. A megoldást most a képlet használatára és a jelölések szöveg alapján történő értelmezésére építettük fel. Ha helyesen meg tudjuk határozni a feladat típusát, akkor a képletet a függvénytáblázatból is kikereshetjük. A visszatevés nélküli modellre vonatkozó képlet a Hipergeometrikus eloszlás címszónál található meg.
Kulcsmondat: valószínűség egy elméleti érték, a relatív gyakoriság egy kísérleti mérőszám
A valószínűség és a relatív gyakoriság szorosan összefüggő fogalmak a matematikában és a statisztikában. A valószínűség egy elméleti érték, amely egy esemény bekövetkezésének mértékét fejezi ki, míg a relatív gyakoriság egy kísérleti mérőszám, amely azt mutatja meg, hogy egy adott esemény hányszor következik be egy adott számú ismétlés során.
A relatív gyakoriság azt mutatja meg, hogy egy adott esemény hányszor következik be egy adott számú kísérlet során. Matematikailag így számítható:
A valószínűség egy elméleti fogalom, amely megadja egy esemény bekövetkezésének esélyét, ha minden kimenetel egyformán valószínű. Egy esemény valószínűsége a következőképpen számítható:
Kulcsmondat: az eredmény valószínűségekkel súlyozott átlaga
A várható érték egy valószínűségi változó súlyozott átlaga, amely megmutatja, hogy egy bizonytalan kimenetelű helyzetben hosszú távon milyen eredményre számíthatunk. Ez egy fontos eszköz a különböző modellek, játékok és döntési helyzetek összehasonlítására, különösen akkor, ha az egyes modelleken belül az események eltérő valószínűségekkel fordulnak elő.
A várható érték segítségével például két szerencsejátékot vagy befektetési lehetőséget is összehasonlíthatunk: bár mindkettő eltérő kimenetelekkel és esélyekkel rendelkezhet, a várható érték alapján eldönthető, hogy hosszú távon melyik a kedvezőbb. Ezért a várható érték nemcsak a statisztikában és a valószínűségszámításban, hanem a gazdasági döntéshozatalban, a biztosítási matematikában és a stratégiai tervezésben is kulcsszerepet játszik.
| Összeg | Gyakoriság |
| 2 | 1 |
| 3 | 1 |
| 4 | 3 |
| 5 | 4 |
| 6 | 6 |
| 7 | 8 |
| 8 | 5 |
| 9 | 4 |
| 10 | 4 |
| 11 | 3 |
| 12 | 2 |
| Összeg | Gyakoriság | Lehetséges dobások | Relatív gyakoriság | Valószínűség |
| 2 | 1 | \(1+1\) | \(\dfrac{1}{41}\) | \(\dfrac{1}{36}\) |
| 3 | 1 | \(1+2,\;2+1\) | \(\dfrac{1}{41}\) | \(\dfrac{2}{36}\) |
| 4 | 3 | \(1+3,\;2+2,\;3+1\) | \(\dfrac{3}{41}\) | \(\dfrac{3}{36}\) |
| 5 | 4 | \(1+4,\;2+3,\;3+2,\;4+1\) | \(\dfrac{4}{41}\) | \(\dfrac{4}{36}\) |
| 6 | 6 | \(1+5,\;2+4,\;3+3,\;4+2,\;5+1\) | \(\dfrac{6}{41}\) | \(\dfrac{5}{36}\) |
| 7 | 8 | \(1+6,\;2+5,\;3+4,\;4+3,\;5+2,\;6+1\) | \(\dfrac{8}{41}\) | \(\dfrac{6}{36}\) |
| 8 | 5 | \(2+6,\;3+5,\;4+4,\;5+3,\;6+2\) | \(\dfrac{5}{41}\) | \(\dfrac{5}{36}\) |
| 9 | 4 | \(3+6,\;4+5,\;5+4,\;6+3\) | \(\dfrac{4}{41}\) | \(\dfrac{4}{36}\) |
| 10 | 4 | \(4+6,\;5+5,\;6+4\) | \(\dfrac{4}{41}\) | \(\dfrac{3}{36}\) |
| 11 | 3 | \(5+6,\;6+5\) | \(\dfrac{3}{41}\) | \(\dfrac{2}{36}\) |
| 12 | 2 | \(6+6\) | \(\dfrac{2}{41}\) | \(\dfrac{1}{36}\) |
| Összeg | 41 | 36 | 1 | 1 |
Kulcsmondat: két szakasz hosszának vagy két síkidom területének hányadosát keressük
A geometriai valószínűség kiszámítása hasonlóan történik, mint a klasszikus valószínűség esetében. Először megkeressük azt a geometriai alakzatot, ahol az események történhetnek, majd azt, amely helyeken történt eseményeket kedvezőnek tekintjük. Ha szakaszokról van szó, akkor ezek hosszát, ha síkidomokról, akkor ezek területét kell meghatároznunk. A kapott mérőszámok hányadosa fogja adni a keresett valószínűséget.
A feladatok nehézségét általában nem a ponthalmazok méretének meghatározása jelenti, hanem maguknak a ponthalmazoknak a meghatározása. Az egyszerűbb esetekben, a ponthalmazok könnyen azonosíthatóak, mint a mellékelt feladatban is. A következő oldalakon két példát fogunk nézni, amelyekben a számegyenest és a koordináta-rendszert is segítségül hívjuk.
A geometriai valószínűség kiszámítása során általában nem lényeges, hogy szakaszok esetén azok végpontjai, illetve síkidomok esetén azok határoló vonalai kedvező eseményhez tartoznak vagy sem. Szakasz esetén a határoló pont "hossza" \(0\), így az nem jelent változást a számláló kiszámításában. Hasonlóan síkidomok esetén a határolóvonal a területhez nem ad hozzá, így az sem fontos a valószínűségszámítás szempontjából, hogy ezek melyik eseményhez tartoznak.
Kulcsmondat: konvertáljuk az időt intervallummá
A feladatról első ránézésre nem látszik, hogy a geometriai valószínűség eszközei használhatóak, ugyanis nem láthatóak közvetlenül a ponthalmazok. Ebben az esetben a ponthalmazokat intervallumok fogják alkotni és az időt fogjuk ábrázolni számegyenesen. Önmagában természetes módja az idő ábrázolásának, hogy egy vonal mentén bejelöljük az időpontokat úgy, hogy az így keletkezett szakaszok hossza arányos legyen az idő hosszával.
Az ábrázolás lényegében már elvezet a megoldáshoz, bár a kedvezőnek tekintendő időszakok megjelölése gyakran nem ennyire egyszerű, mint a mellékelt példában. Ebben az esetben csak a kritikus időpontokat kell kijelölni, amikor Kata a telefonjára pillant és ezekhez a megfelelő oldalra illeszteni a 10 perces időszakokat. Mivel az üzenetnek előbb kell érkezni, mint ahogyan Kata megnézi a telefonját, így a 10 perces intervallumokat az adott időpontoktól balra helyezzük el.
Az események megfigyelt időszaka is fontos szerepet kap, ugyanis az első időszak nem 10 perc hosszú lesz. Az események bekövetkezése (az üzenet megérkezése) csak 17:00 és 18:00 között érdekes, így csak azok a lehetőségek érdekelnek bennünket, amelyek ezen az időszakon belül vannak.
Kulcsmondat: két "mozgó" időpont ábrázolását koordináta-rendszerben tehetjük meg
Az előző feladatban az egyik időpont rögzített volt, ugyanis Kata ismert időpontban pillantott a telefonjára. A másik időpont véletlenszerűen változott. Ha mindkét időpont véletlenszerűen változhat (két valószínűségi változóval dolgozunk), akkor a számegyenes már nem elegendő. A megoldást a koordináta-rendszer adja, amely két egymásra merőleges számegyenesnek tekinthető.
A feladatban a két kiránduló érkezésének időpontja véletlenszerű, azonban a kedvező esemény (amikor találkoznak) hossza adott a feladatban (10 perc). A koordináta-rendszer tengelyeit most két idővonalnak tekintjük, ahol a koordináták a két kiránduló érkezési ideje 14:00 után perben mérve.
Ennyi már elegendő is, hogy az origóbil kiindulva 60-60 percet jelző négyzeten belül megkeressük azokat a pontokat, amelyek koordinátái a kedvező időpontokat jelölik. Ez a megoldási módszer összetettebb ponthalmazok esetén is jól működik.
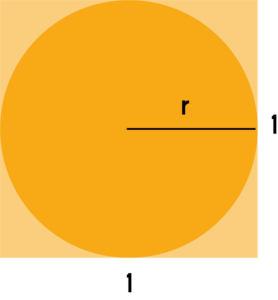Határozzuk meg azon pontok halmazát, amelyek kisebb távolságra vannak a négyzet
átlóinak metszéspontjától, mint \(\dfrac{1}{2}\), azaz az oldalhossz felénél. Jelöljük az állók
metszéspontját \(O\)-val, amelytől a \(\dfrac{1}{2}\)-nél közelebb eső pontok halmaza, egy olyan körlap,
amelynek középpontja \(O\) és sugara \(r=\dfrac{1}{2}\). A keresett valószínűség a körlap és a négyzet
területének hányadosa.
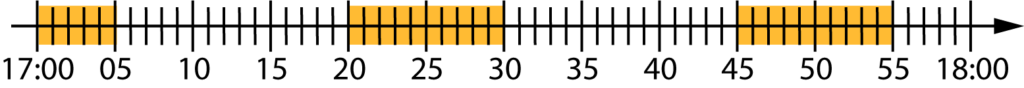
Copyright © iMatek 2020-2025 – Minden jog fenntartva
