
Matematikai érdekességek, amelyek jól jöhetnek az érettségin vagy a felvételin is.

A titkosítás lényege az, hogy a beavatott személyek úgy tudjanak egymásnak üzenetet küldeni, hogy bármely üzenetet el tudjanak olvasni, azonban egyetlen kívülálló se ismerhesse meg a tartalmat, illetve ne lehessen más nevében hamis üzenetet küldeni. A régebbi titkosítások meglehetősen egyszerűek voltak, amelyek közül néhány már inkább egy rejtvényújság feladványa lehetne, mintsem biztonságos kriptográfiai megoldás.
Egy rövid történeti kitérő után áttekintünk két modern titkosítási módszert, az RSA és az elliptikus görbéken alapuló kódolást. Az utóbbi két módszer matematikai háttere lényegesen meghaladja az emelt szintű középiskolai érettségi követelményeit, ennek ellenére sokak számára érdekesek lehetnek. A kíváncsiságunkat az is táplálja, hogy a mindennapokban gyakran találkozunk a kriptovalutákkal, blockchain-nel és elektronikus aláírással Az alábbiakban áttekintendő kódok akár nemzetbiztonsági szintű rejtjelezésre is alkalmasak.
Valóban fontos kérdés: Fel tudjuk törni a titkosítást? A válasz lényegében csak annyi tud lenni, hogy a mai technológia mellett jelenleg tudunk olyan titkosítást készíteni, amely reális időn belül nem törhető fel. Azt viszont nehéz megmondani, hogy a kvantumszámítógépek korában milyen titkosítási módszereket kell majd kialakítani.
 A kódolás lényege, hogy minden résztvevőnek meg kell állapodnia egy kódrendszerben, amely a sikeres dekódolás kulcsa. Fel tudjuk törni? Vélhetően igen. Sokszor sikeres feltörést eredményez, ha gyakran előforduló vagy az adott szövegben gyakran ismétlődő betűket szavakat keresünk, például “az”, “egy” stb.
A kódolás lényege, hogy minden résztvevőnek meg kell állapodnia egy kódrendszerben, amely a sikeres dekódolás kulcsa. Fel tudjuk törni? Vélhetően igen. Sokszor sikeres feltörést eredményez, ha gyakran előforduló vagy az adott szövegben gyakran ismétlődő betűket szavakat keresünk, például “az”, “egy” stb.
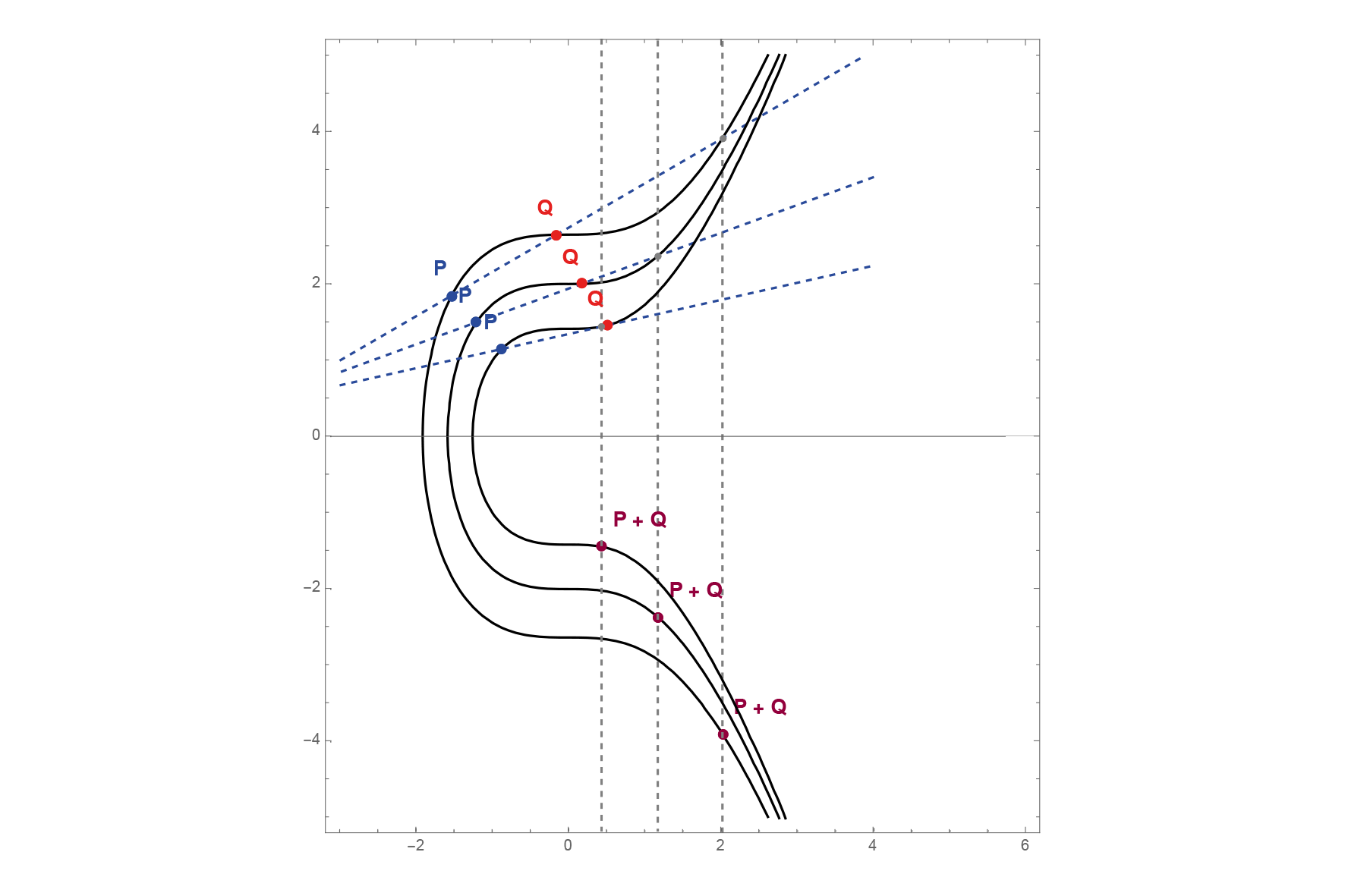
 Most egy nehéz lépés jön. Műveleteket értelmezünk az elliptikus görbe pontjai között. Először két pont összegét, \(P+Q\)-t, majd egy pont skalárszorosát, \(nP\)-t definiáljuk. Két különböző pont összege legyen az ábrán jelölt \(P+Q\), azaz \(P,Q\)-n átmenő egyenes és a görbe metszéspontját tükrözzük az \(x\) tengelyre.
Most egy nehéz lépés jön. Műveleteket értelmezünk az elliptikus görbe pontjai között. Először két pont összegét, \(P+Q\)-t, majd egy pont skalárszorosát, \(nP\)-t definiáljuk. Két különböző pont összege legyen az ábrán jelölt \(P+Q\), azaz \(P,Q\)-n átmenő egyenes és a görbe metszéspontját tükrözzük az \(x\) tengelyre.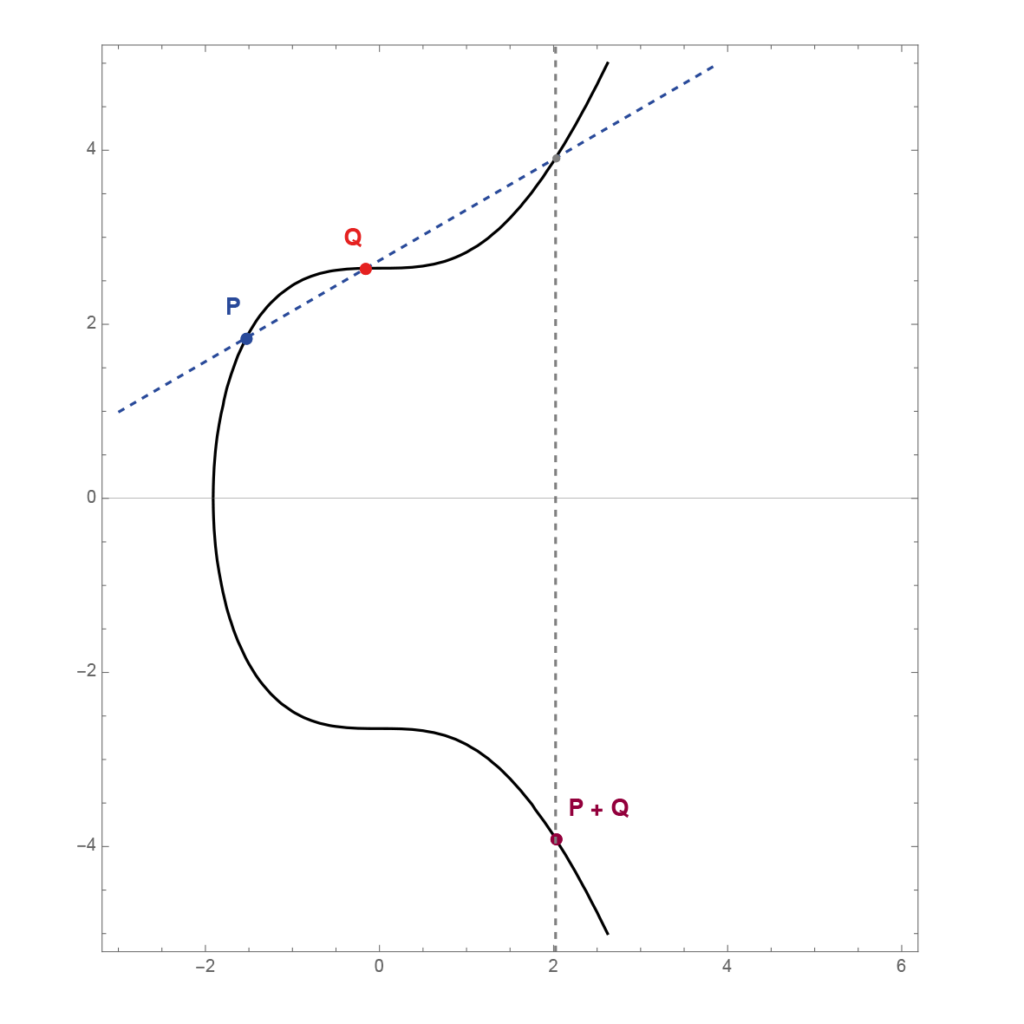 Egy pont kétszeresét, \(2P\)-t úgy kapjuk, hogy \(P\)-ben érintőt húzunk az elliptikus görbéhez, és a görbével vett metszéspontját tükrözzük \(x\) tengelyre.
Egy pont kétszeresét, \(2P\)-t úgy kapjuk, hogy \(P\)-ben érintőt húzunk az elliptikus görbéhez, és a görbével vett metszéspontját tükrözzük \(x\) tengelyre. A műveletek szokatlanok lehetnek, de talán ez adja az érdekességüket is. Ha meghatározzuk a \(2^kP\) pontokat, akkor ebből már tetszőleges \(nP\) pont számítható. Erre azért van szükség, mert kevesebb művelettel számítható ki egy pont tetszőleges skalárszorosa, \(nP\), ahhoz viszonyítva, mintha az \(n\) db összeadást elvégeznénk. Például \(9P=2^3P+P\), így a 9 összeadás helyett csak három duplikációt és egy összeadást kellett elvégezni. Ennek azért van jelentősége, mert nagyon nagy számokkal dolgozik a titkosító algoritmus, és az alacsonyabb műveletigény növeli a számítás sebességét.
A műveletek szokatlanok lehetnek, de talán ez adja az érdekességüket is. Ha meghatározzuk a \(2^kP\) pontokat, akkor ebből már tetszőleges \(nP\) pont számítható. Erre azért van szükség, mert kevesebb művelettel számítható ki egy pont tetszőleges skalárszorosa, \(nP\), ahhoz viszonyítva, mintha az \(n\) db összeadást elvégeznénk. Például \(9P=2^3P+P\), így a 9 összeadás helyett csak három duplikációt és egy összeadást kellett elvégezni. Ennek azért van jelentősége, mert nagyon nagy számokkal dolgozik a titkosító algoritmus, és az alacsonyabb műveletigény növeli a számítás sebességét.
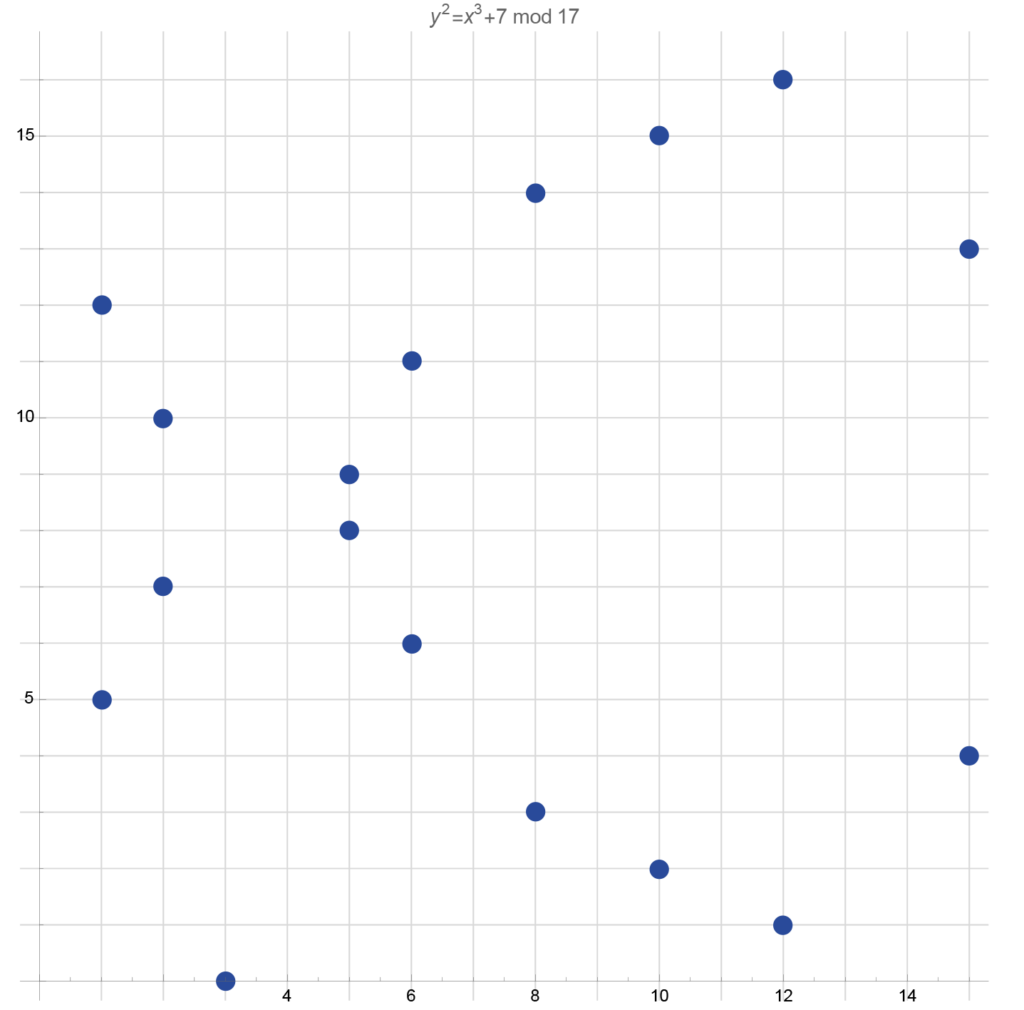 Igen, ez se nem elliptikus, se nem görbe.
A grafikonról leolvasható, hogy például az \((1,\,5)\) pont eleme a diszkrét elliptikus görbének, mert
\[
\begin{aligned}
x^3+7=1^3+7=7,\quad 7\equiv 7 \mod 17\\
y^2=5^2=25,\quad 25\equiv 7\mod 17
\end{aligned}\notag
\]
Azaz a diszkrét elliptikus görbe egyenletét kielégítik a megadott koordináták (\(17\)-tel vett maradékait tekintve).
Igen, ez se nem elliptikus, se nem görbe.
A grafikonról leolvasható, hogy például az \((1,\,5)\) pont eleme a diszkrét elliptikus görbének, mert
\[
\begin{aligned}
x^3+7=1^3+7=7,\quad 7\equiv 7 \mod 17\\
y^2=5^2=25,\quad 25\equiv 7\mod 17
\end{aligned}\notag
\]
Azaz a diszkrét elliptikus görbe egyenletét kielégítik a megadott koordináták (\(17\)-tel vett maradékait tekintve).

 Copyright © iMatek 2020-2025 – Minden jog fenntartva
Copyright © iMatek 2020-2025 – Minden jog fenntartva