iMatek

Sejtautomaták – rend vagy káosz

  • hatványozás, logika, sejtautomata, számrendszerek

Mire jó a Matek?

Picture of matematikai alkalmazások

matematikai alkalmazások

Matematikai érdekességek, amelyek jól jöhetnek az érettségin vagy a felvételin is.

Alkalmazások
ca_rainbow

Oszd meg, ha tetszik!

Rend vagy káosz?

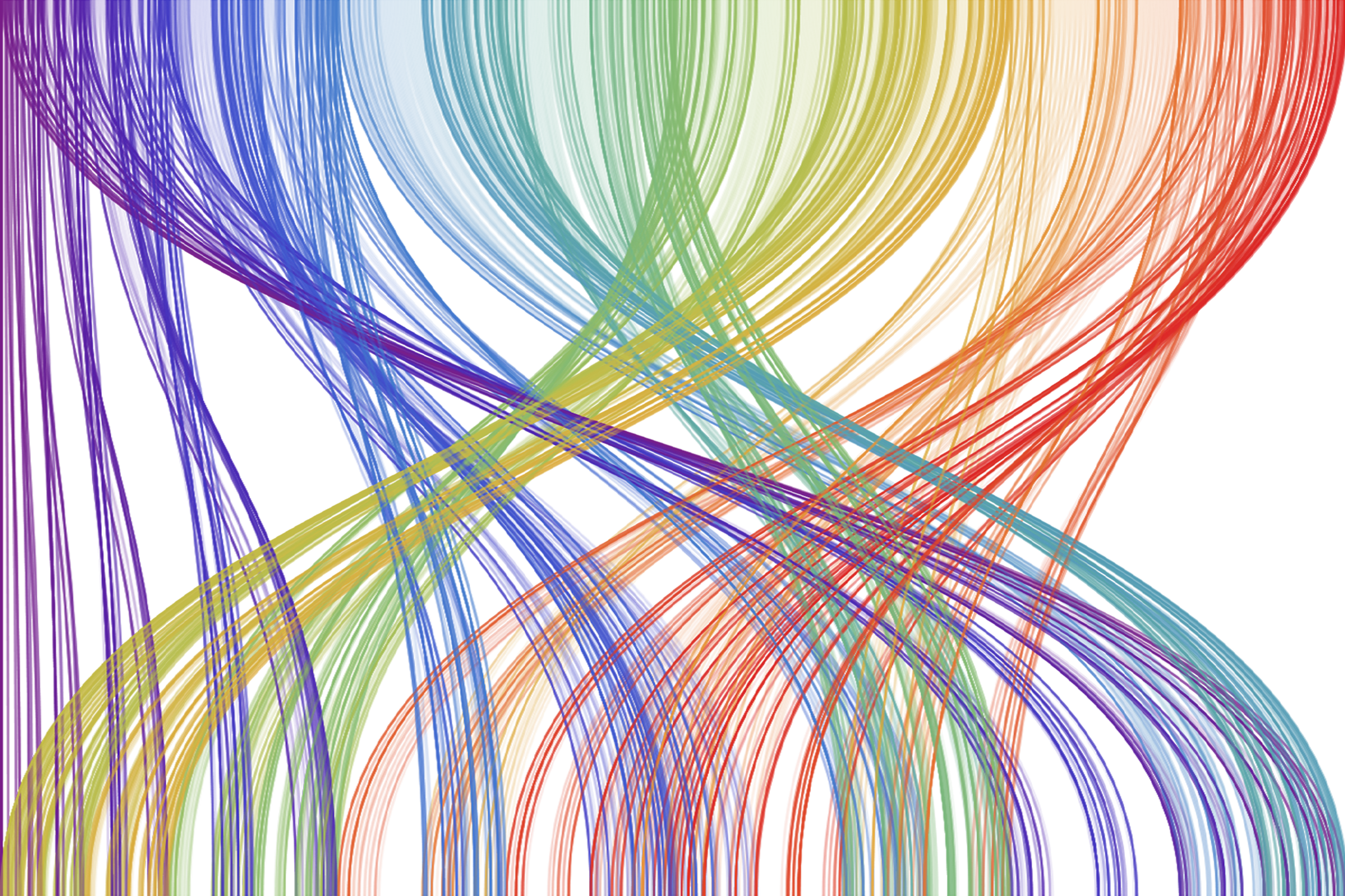
Ez az ismertető a Közlekedési forgalom modellezés bejegyzés folytatása, ezért ha a sejtautomaták nem ismerősek, akkor célszerű az ottani bevezetőt megismerni, mielőtt tovább olvasod ezt a cikket.

Absztrakt képek
Korábbi bejegyzésben már áttekintettük a sejtautomaták működését, az elemi sejtautomaták csoportjait. Arra keressük a választ, hogy hogyan tudjuk szemléltetni egyes elemi sejtautomaták véletlenszerű illetve komplex viselkedését.
Nézzük először a \(30\)-as szabályt, amelyről tudjuk, hogy véletlenszerűen viselkedik, amely tulajdonságát kihasználva véletlenszám generátorként is használják. A \(30\)-as szabály onnan kapta a nevét, hogy a \(8\) lehetséges kiinduló állapot által meghatározott \(8\) állapota az új generációnak az alábbi módon került felírásra. (Ha a sejtautomata egy lépés utáni képét tekintjük, és a korábban megismert módon kettes számrendszerbe írjuk át, akkor \(00011110_2=30\).)

Korábban már áttekintettük az elemi sejtautomaták klasszikus ábrázolását, amikor egy véges négyzethálón (négyzet vagy téglalap), a felső sorban véletlenszerűen veszünk fel értékeket, majd a megadott \(30\)-as szabály szerint több lépést ábrázolunk lefelé.

Az ábrán is jól látható a kaotikus viselkedés, amelyet tovább erősít a kirajzolódó háromszögek eltérő mérete és rendezetlen elhelyezkedése.
Káosz

A rendezettség és a káosz szemléltetésére bevezetünk egy új ábrázolási módot. Tekintsünk most egy olyan elemi sejtautomatát, amely \(10\) egymás melletti négyzethez rendel hozzá egy másik \(10\) hosszúságú, új generációt leíró sort. A szabályokat a korábban leírt \(256\) féle szabályból választjuk. Először a fentiekben definiált \(30\)-as szabályt nézzük meg. Ha több lépésben alkalmazzuk egymás után ugyanazt a szabályt, mint ahogyan azt már a fenti ábra elkészítésénél is tettük, akkor előre tudunk lépdelni, ami az ábrán azt jelenti, hogy lefelé haladunk. Minden sort egyértelműen tudunk származtatni a megelőző sorban megjelenített sejtek állapotából. Visszafelé azonban nem vezet egyértelmű út, nem tudjuk egyértelműen visszafejteni, hogy mi is lehetett a korábbi állapot. Egy későbbi generációt leíró állapotból nem minden estben tudjuk meghatározni a korábbiakat.

Egy-egy szabály hatását szeretnénk modellezni oly módon, hogy a korábban említett \(10\) hosszúságú sor minden lehetséges felírásához hozzárendeljük a sejtautomata által létrehozott képét. Kezdjük azzal, hogy megfeleltetünk egy kettes számrendszerben felírt számot minden állapotnak, oly módon, hogy a fehér négyzeteket \(0\)-val, a feketéket pedig \(1\)-gyel jelöljük az \(10\) hosszúságú négyzetháló sorban. Az első néhány elemet fel is írhatjuk: \(0000000000_2\), \(0000000001_2\), \(0000000010_2,\ldots\). Ennek a sorozatnak \(2^{10}=1024\) eleme van. Ha egymás alá rendezve kétszer felírjuk az \(1024-1024\) elemet, akkor ezeket összeköthetjük annak megfelelően, hogy egy kiindulási állapothoz milyen állapotot rendel hozzá az adott szabályrendszerrel működő elemi sejtautomata. Ezeket a vonalakat trajektóriáknak nevezzük.
Nézzünk meg egy megfeleltetést a \(30\)-as szabály szerinti sejtautomatánál. Azaz az egymás mellé rendezett \(1024\) darab \(10\)-es blokk \(289.\) eleméhez a \(499.\) elemet rendeli hozzá. Rajzoljuk meg a teljes sorra a trajektóriákat.
Az ábra nagyon szemléletes. Láthatjuk, hogy egyetlen lépés után mennyire kuszák a trajektóriák. Ezzel találtunk egy olyan ábrázolási módot, amely a sejtautomata egy lépését szemlélteti a kezdeti feltételek teljes halmazán.
Nézzük meg most mi történik, ha egymás után ötször alkalmazzuk a sejtautomata lépéseit.

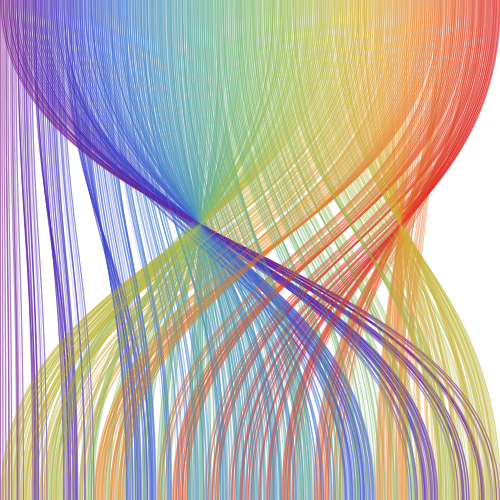
Vörössel jelöltünk egy \(50\) egységből álló tartományt, azaz \(50\) darab, egymást követő, tízjegyű kettes számrendszerben felírt számhoz és a képéhez tartozó trajektóriát. Mindamellett, hogy ez a kép is vetekszik egy modern absztrakt képpel, jól látható, hogy már öt lépést követően, az egymás melletti számok képe lényegében a teljes alsó intervallumon szétterül. Ezzel sikerült két olyan ábrázolási módot készíteni, amelyről leolvasható, hogy egy elemi sejtautomata mennyire viselkedik rendezetten vagy véletlenszerűen.

Az utolsó két ábra jól szemlélteti a \(30\)-as szabály kaotikusságát, és jól ábrázolja, hogy miért alkalmas ez a sejtautomata akár véletlenszám generátornak is. A vörössel jelölt trajektóriák azt is jól mutatják, hogy az első lépés még nem nagyon váltak el, azaz viszonylag rendezett maradt. A másodikban azonban határozottan kettéválik a vonalsereg, majd ezt követően egyre kevesebb rendszert figyelhetünk meg.
Az alábbiakban bemutatjuk még a klasszikus háromszög rajzot, ugyanezen sejtautomatához.
További példák
\(15\)-ös szabály

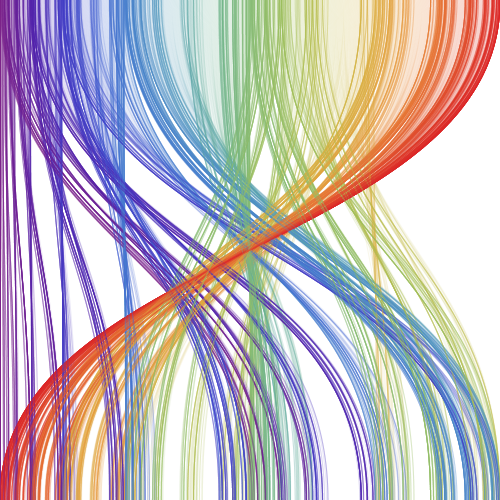
\(54\)-es szabály

\(71\)-es szabály

\(90\)-es szabály

\(106\)-os szabály

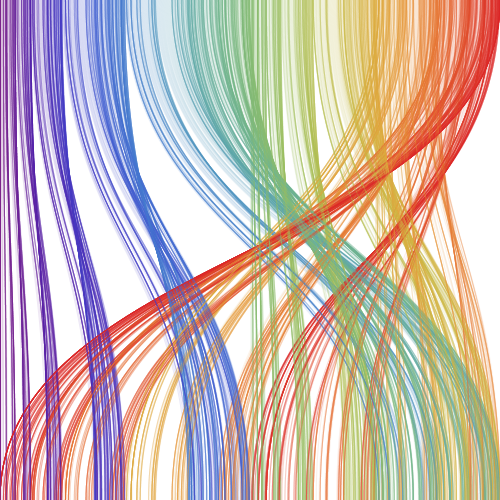
\(110\)-es szabály

\(118\)-as szabály

\(210\)-es szabály

Biológiai mintázatképződés
Az absztrakt képek után térjünk át a sejtautomaták egy alkalmazási lehetőségére a biológiában. Gyakran találkozunk a természetben különböző mintákkal, legyen az kagyló vagy csigaház, puhatestűek, halak, kétéltűek, madarak vagy emlősök.
A legegyszerűbb (egy-dimenziós) elemi sejtautomata néhány mintázatát már vizsgáltuk, azonban pillantsunk rá ezekre ismét, más szemszögből. Az elemi sejtautomaták jól modellezik a csiga és kagylóhéjak mintázatát, a hasonlóság pedig meghökkentő. Az első képen látható kúpcsiga házának a mintázata rendkívüli hasonlóságot mutat az alábbi ábrákon látható sejtautomaták által létrehozott mintázatokkal.

Természetesen bonyolultabb mintázatok is kialakulnak, amelyek már nehezen modellezhetők az elemi egy-dimenziós sejtautomatákkal. A nagymacskák és a zebra esetén olyan két-dimenziós modellt használhatunk, amely szabályrendszere is összetettebb. Egy adott sejt állapotát a közvetlen szomszédai \(100\%\)-os valószínűséggel befolyásolják, azonban kisebb valószínűséggel a második, illetve harmadik szomszédos sejtek állapotát is figyelembe vehetjük. A négyzethálónk ebben az esetben már két dimenziós, így lehetőségünk van arra is, hogy a modellben a szomszédos sejtek állapotát csak egy irányból (vízszintesen vagy függőlegesen), esetleg mindkét irányból beépítsük a szabályrendszerbe. A részletes szabályrendszer ismertetésétől eltekintünk, de nézzünk néhány példát az előzőekben leírt sejtautomata mintázataira. Az első ábrán csak vertikális szabályt használtunk, míg a másik kettőn kétirányút. (A sejtautomaták a kezdeti véletlenszerűen felvett pontokból körülbelül 10 lépésben jutottak el az alábbi elrendeződésig.)
5. Becslések – Egyetemi statisztika
Statisztikai becslések
2025

5. Becslések – Egyetemi statisztika

990 Ft
(Az ár tartalmazza a 27% ÁFA-t)
A kurzus lejárata:
2025. július 15.
                        Részletek Vásárlás
6. Hipotézisvizsgálat – Egyetemi statisztika
Hipotézisvizsgálat
2025

6. Hipotézisvizsgálat – Egyetemi statisztika

990 Ft
(Az ár tartalmazza a 27% ÁFA-t)
A kurzus lejárata:
2025. július 15.
                        Részletek Vásárlás

Kapcsolat

Dokumentumok

Pénzügyi Partnerünk

CIB Bank

Elfogadott kártyák

Bankkártyák

Vásárlási kisokos

    Írj nekünk!



    Első kép Második kép
    Facebook Map-marker-alt Tiktok

    Ügyfélszolgálat

    • Telefon: +36 30 427-6190
    • hétfő-péntek: 8:00-16:00
      Copyright © iMatek 2020-2025 – Minden jog fenntartva