
A matematikai megértés fázisai
Ha megértesz egy példát, akkor az sokszor csak a kezdet.

A sikeres tanuláshoz nem csak a tudásra van szükség.

|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
\color{red}{A}&C&D&B\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
\color{red}{A}&D&B&C\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
C&\color{red}{B}&D&A\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
D&\color{red}{B}&A&C\\
\hline
\end{array}\notag
\]
|
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
B&D&\color{red}{C}&A\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
D&A&\color{red}{C}&B\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
B&C&A&\color{red}{D}\\
\hline
\end{array}\notag
\]
|
\[
\begin{array}{|c|c|c|c|}
\hline
A&B&C&D\\
\hline
C&A&B&\color{red}{D}\\
\hline
\end{array}\notag
\]
|

| Tevékenység | Diákok száma (fő) | Középponti szög |
| Sport | \(30\) | \(135°\) |
| Olvasás | \(20\) | \(\boldsymbol{\color{green}{90°}}\) |
| Zenehallgatás | \(15\) | \(67,5°\) |
| Számítógépes játékok | \(10\) | \(\boldsymbol{\color{green}{45°}}\) |
| Filmnézés | \(\boldsymbol{\color{green}{5}}\) | \(22,5°\) |
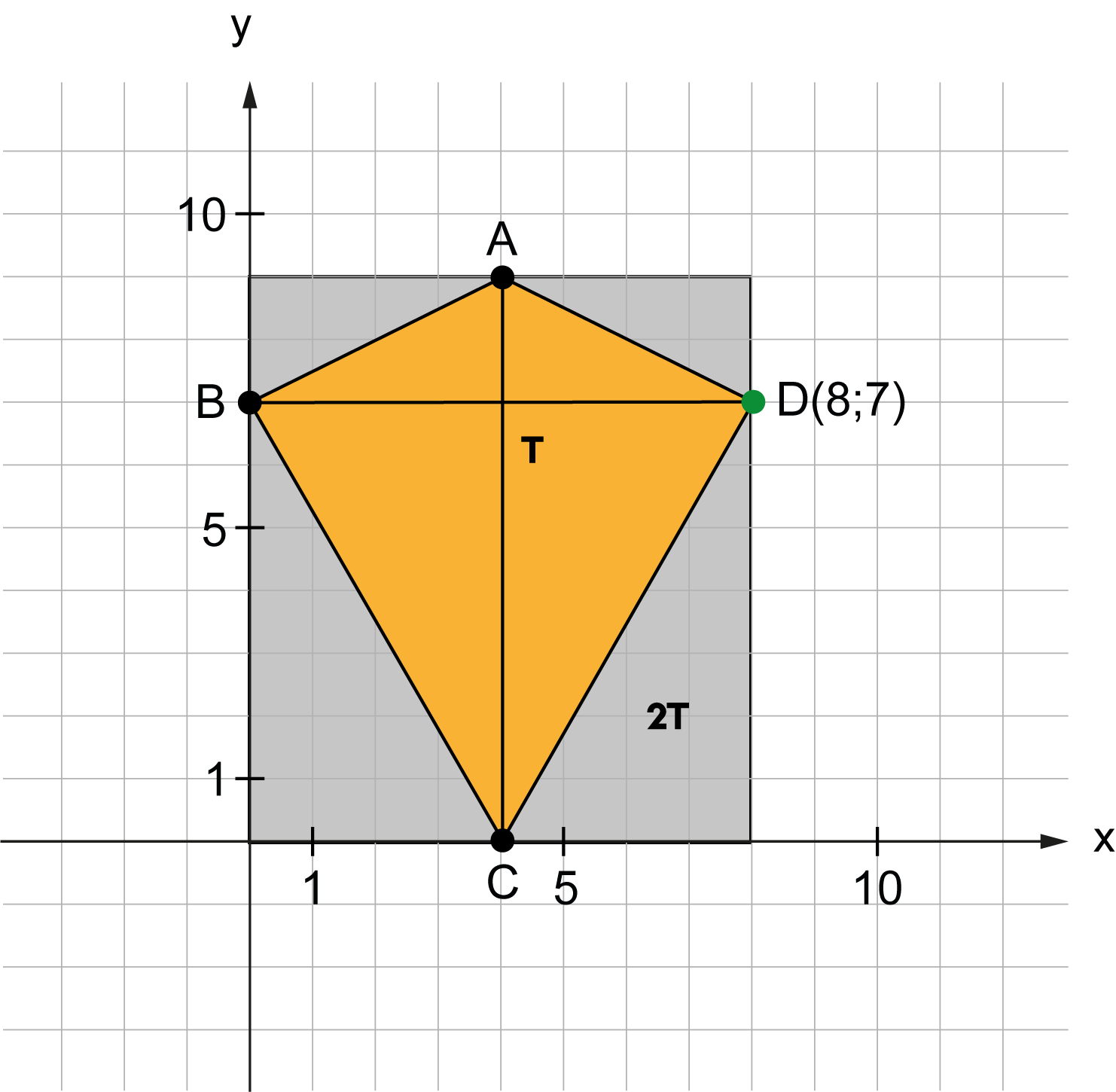

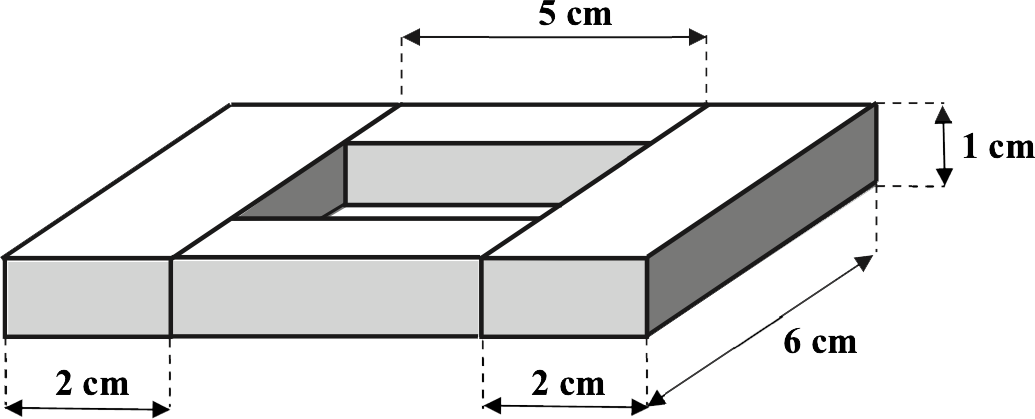

Ha megértesz egy példát, akkor az sokszor csak a kezdet.
 Copyright © iMatek 2020-2025 – Minden jog fenntartva
Copyright © iMatek 2020-2025 – Minden jog fenntartva