iMatek

Statisztikával a manipuláció ellen II.

  • binomiális eloszlás, konfidencia intervallum, statisztika, szignifikancia szint

Mire jó a Matek?

Picture of matematikai alkalmazások

matematikai alkalmazások

Matematikai érdekességek, amelyek jól jöhetnek az érettségin vagy a felvételin is.

Alkalmazások
histogram_2_true1

Oszd meg, ha tetszik!

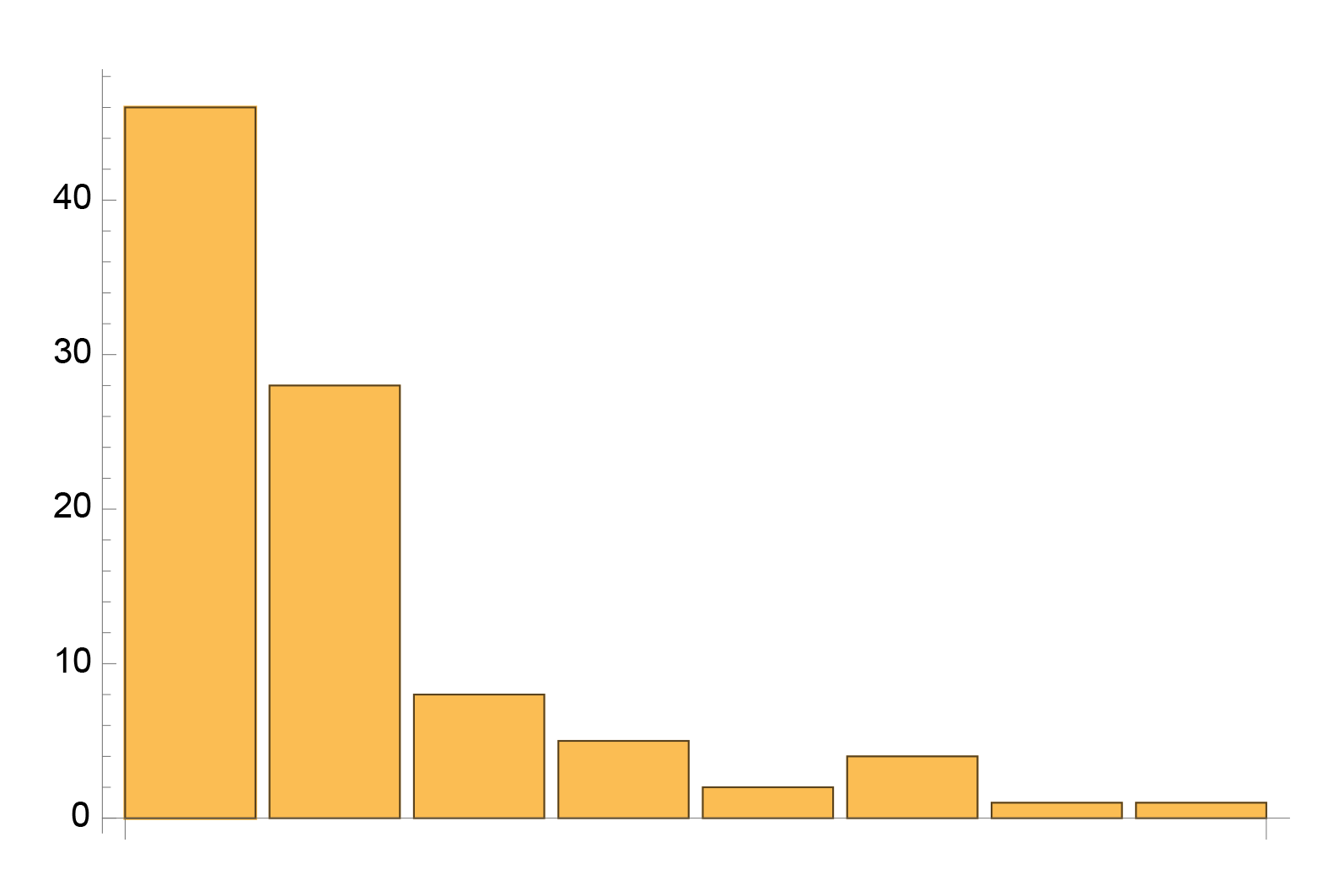
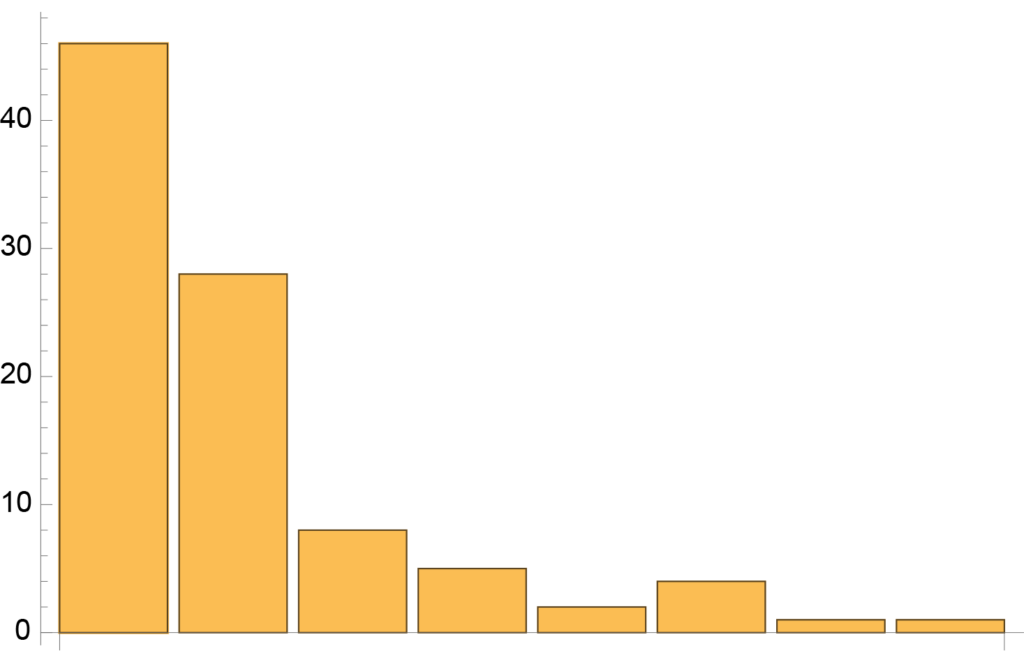
Az előző matematikai alkalmazás statisztikai leírásban részletesen megvizsgáltuk, hogy ha az elméleti várakozásunk binomiális eloszlás szerint kell, hogy alakuljon, akkor ez nem jelenti azt, hogy pontosan aszerint is alakul, sőt az a gyanús, ha  pontosan azt az eredményt kapjuk, esetünkben az 50-50%-os fej-írás kimenetet a pénzfeldobásnál.

A korábbi leírásban egy gépi véletlenszám generátort használtunk, amely jól közelíti a tényleges pénzfeldobást. Most egy olyan “kísérlet” eredményét  is beillesztjük, amelyet az egyesek és nullák manuális soraként kaptunk meg. Azt vizsgáljuk tovább, hogy van-e más gyanús jele a hamis sorozatnak.

A túl nagy rendetlenség árulkodó

A fenti sorozat első ránézésre rendben lévőnek tűnik, az egyesek és nullák véletlenszerűnek tűnő sorrendben követik egymást. Az egyetlen “gyanús” eredmény, hogy pont 100 darab 1-es és 100 darab 0 szerepel a felsorolásban, aminek a korábbiak alapján tudjuk, hogy csak 5% körüli az esélye.

A pontos valószínűséget az alábbiakból számíthatjuk ki.
\[
P(X=100)=\frac{\binom{200}{1}}{2^{200}}\approx 0,0563
\notag
\]
A valószínűséget felírhattuk volna a binomiális eloszlás képlete alapján is, de az 50-50%-os fej-írás kimenet miatt inkább a Pascal-háromszöget használtuk. A fej dobások száma a 200. sor középső eleme, amely \(\binom{200}{100}\), az összes esemény pedig a Pascal-háromszög 200. sorában található binomiális együtthatók összege, amelyről a felkészítőben belátjuk, hogy összege éppen \(2^{200}\). Persze egyszerű kombinatorikai módon is megfogalmazhatjuk a fentieket.
Egy véletlenszerűen kialakított \(1-0\) sorozatban további vizsgálatokat végezhetünk az egyes értékek egymásutániságát elemezve. Bontsuk fel először a valódi pénzfeldobás eredményét párokra: \(\{1,1\},\{0,1\},\{0,0\},\{0,0\},\{0,0\},\{0,0\},\ldots\), majd tegyük meg ugyanezt a manuálisan készítettel is: \(\{0,0\},\{1,1\},\{0,0\},\{0,1\},\{1,0\},\{1,1\},\ldots\). A felbontásban négy fajta elem szerepelhet: \(\{1,1\},\{0,1\},\{1,0\},\{0,0\}\) és szabályos pénzfeldobás esetén ezek mindegyike azonos valószínűséggel, gyakorisággal kell, hogy szerepeljen a sorozatban. Nézzük meg a példáinkban, hogy hogyan alakulnak a gyakoriságok, és ábrázoljuk hisztogrammal!
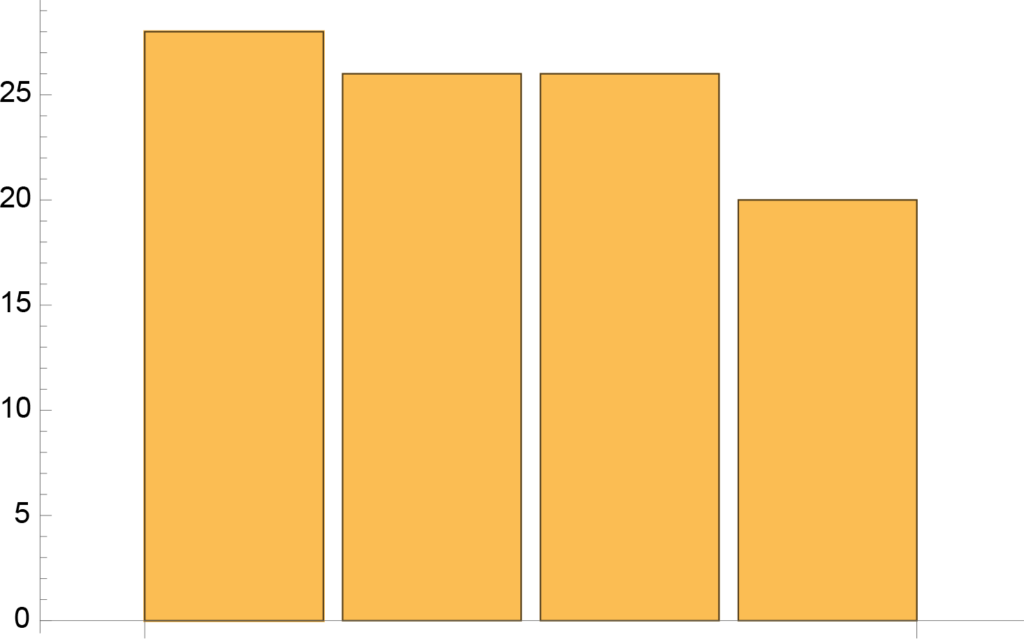
Valódi pénzfeldobás eredménye
\(\{1,1\}\) 28 db
\(\{0,1\}\) 26 db
\(\{0,0\}\) 26 db
\(\{1,0\}\) 20 db
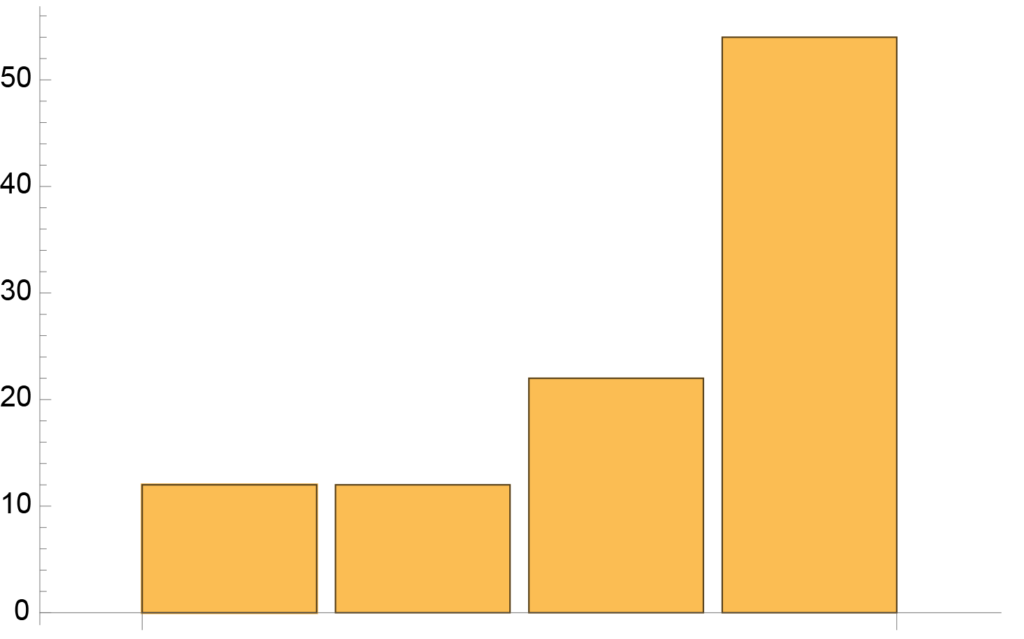
Azt tapasztalja, hogy mind a négy típusú párból 20-28 darab volt a mintában, amely jól közelíti az elméletileg várt 25 darabot. Nézzük most a “hamis” adatsort!
Hamis pénzfeldobás eredménye
\(\{0,0\}\) 12 db
\(\{1,1\}\) 12 db
\(\{0,1\}\) 22 db
\(\{1,0\}\) 54 db
Már elsőre szembeötlő, hogy közel 5-szörös az \(\{1,0\}\) pár előfordulása a \(\{0,0\}\) párhoz képest. Az elméleti modell alapján itt is 25 körüli értékeket szeretnénk látni, hogy meggyőző legyen a szabályosság. Ennek ellenére több mint dupla gyakorisággal is találkoztunk a mintában. Ez egy újabb intő jel, amely alapján a valódiságát megkérdőjelezhetjük a második adatsornak.
Természetesen mehetünk tovább! Vizsgálhatjuk a hármas, vagy a négyes csoportokat is. Az elv megegyezik a fentiekkel, csak a hármasok esetén kilenc féle elem szerepelhet: \(\{1,1,1\},\{0,1,1\},\{1,0,1\},\{1,1,0\},\ldots\), amelyek előfordulási valószínűsége \(\frac{1}{9}\). A jelenlegi mintánk a hármas csoporthoz már meglehetősen kicsi, így itt már nehezen vizsgálható az elvárt gyakoriság megléte.
A csoportosítás más módszerrel is elvégezhető. Tekintsük az egymást követő azonos számjegyek sorozatát, és képezzünk úgy csoportot, hogy minden számjegy váltásnál húzzuk meg a határt. A valós pénzfeldobásos mintában a csoportosítás: \(\{1,1\},\{0\},\{1\},\{0,0,0,0,0,0,0,0,0\},\{1,1,1\},\ldots\) Ehhez nem tudunk olyan eloszlást rendelni, amely könnyű elemzést ígérne, azonban ha összeszámoljuk az \(1, 2, 3, \ldots\) elemű tagokat, akkor intuíciónk azt súgja, hogy az egyeleműekből több lesz, mint többeleműekből. Nézzük meg a két adatsorhoz tartozó hisztogramokat (ha valamely hosszúságú tag gyakorisága 0, akkor azt kihagyjuk).
A valós pénzfeldobás eredménye:
A manipulált pénzfeldobás eredménye:
Feltűnő, hogy a valós adatsor esetén 8, míg a “hamisban” 5 féle elemhossz szerepel, illetve az egyelemű csoportok is szembetűnő különbséget mutatnak. Valós esetben 46, a “hamis” adatsor esetén pedig 119 darab szerepel.
Ezzel befejeztük az adatok elemzését. A kézzel készült adatsor esetén több “furcsaságot’ láttunk akkor is, amikor nem az egyes eseményeket vizsgáltuk, hanem azokat egymás után rendezve, csoportokat hoztunk létre. Láthattuk, hogy a “hamis” adatsor esetében a véletlenszerűséget azzal próbálták meg elérni, hogy “változatosan” írták egymás mellé az elemeket. A “valódi” véletlen más tulajdonságokkal rendelkezik, keletkeznek olyan hosszabb eseményláncok is, amelyek néha már a manipuláció jeleit mutathatják a laikusok számára. Ilyen eseménysor a valós adatsorban 11 darab egymást követő 1-es!
5. Becslések – Egyetemi statisztika
Statisztikai becslések
2025

5. Becslések – Egyetemi statisztika

790 Ft
(Az ár tartalmazza a 27% ÁFA-t)
A kurzus lejárata:
2025. július 15.
                        Részletek Vásárlás
6. Hipotézisvizsgálat – Egyetemi statisztika
Hipotézisvizsgálat
2025

6. Hipotézisvizsgálat – Egyetemi statisztika

790 Ft
(Az ár tartalmazza a 27% ÁFA-t)
A kurzus lejárata:
2025. július 15.
                        Részletek Vásárlás

Kapcsolat

Dokumentumok

Pénzügyi Partnerünk

CIB Bank

Elfogadott kártyák

Bankkártyák

Vásárlási kisokos

    Írj nekünk!



    Első kép Második kép
    Facebook Map-marker-alt Tiktok

    Ügyfélszolgálat

    • Telefon: +36 30 427-6190
    • hétfő-péntek: 8:00-16:00
      Copyright © iMatek 2020-2025 – Minden jog fenntartva