Statisztikával a manipuláció ellen I.

binomiális eloszlás, konfidencia intervallum, statisztika, szignifikancia szint

Mire jó a Matek?

EscapeCode Adventures
A Logika Igazi Rejtélye

Ha lottóztál már, akkor valószínűleg felmerült benned, hogy a kihúzott számok valóban véletlenszerűek-e. A számokat hosszú évekre visszamenőleg közzéteszik, így ezt bárki ellenőrizheti, ha megfelelő statisztikai ismeretek birtokában van. A lottószámok véletlenszerűségének vizsgálatához, a középiskolai statisztikai anyagot meghaladó ismeretekre van szükség, ezért egyszerűsítünk rajta, és egyes részeredményeket nem igazolunk. Az egyszerűbb példa, amelyet megvizsgálunk, egy pénzfeldobásos eseménysorozat. 200-szor feldobunk egy pénzérmét, és azt vizsgáljuk, hogy ez szabályos-e, illetve fogalmazhatnánk úgy is, hogy a feldobások során nem csalt-e valaki.

Nézzünk egy eredményt, ahol az egyesek jelölik az írást, a nullák pedig a fejet.

Manipulálták-e az adatokat?

Azt szeretnénk megvizsgálni, hogy a fenti sorozat hamisított-e, amely 200 szabályos érmével való pénzfeldobás eredményét írja le. A vizsgálat több lépésből áll, így több aspektusból is megnézzük a sorozat valódiságát. Az összehasonlíthatóság és a szemléletesebb levezetés miatt két sorozatot nézünk meg, az egyik véletlenszerű (megfelel a pénzfeldobástól elvárt eredménynek), a másik azonban manuálisan került felírásra, azaz hamisítvány. A középiskolai tananyag része a valószínűségi eloszlások ismerete, amelyet most ki is fogunk használni. Ha egymástól független eseményeket vizsgálunk, ahol visszatevéssel választunk ki elemeket és az egyes események bekövetkezésének valószínűsége azonos, akkor azt binomiális eloszlással tudjuk leírni. Idézzük fel a definíciót!

Ha az \(X\) valószínűségi változó lehetséges értékeinek halmaza \(\{0,1,2,\ldots ,n\}\), ahol \(n\) pozitív egész, és eloszlása: \[ P(X=k)=\binom{n}{k}p^k(1-p)^{n-k} \notag \] ahol \(0\leqslant p \leqslant 1\) és \(k\in \{0,1,2,\ldots,n\}\), akkor \(X\)-et binomiális eloszlású valószínűségi változónak nevezzük (visszatevéses mintavétel). (Az \(n\) és \(p\) az \(X\) valószínűségi változó paraméterei.)

A valószínűségszámítási háttér mellett most bevezetünk néhány statisztikai fogalmat, amelyeket ugyan nem definiálunk pontosan, de igyekszünk szemléletes leírást adni. Az első a szignifikancia szint. Lényegében arról van szó, hogy az eredmény statisztikai értelemben szignifikáns-e (jelentős, meghatározó), jelöljük \(\alpha\)-val. A szignifikancia szint azt mutatja meg, hogy mekkora a hibás, hamis esemény valószínűsége, amelyből következik, hogy a modellünk annál pontosabb, minél alacsonyabb a szignifikancia szint. Gyakran használnak 5%-os szignifikancia szintet, amely már azt mondja, hogy a statisztikai modellünk “jól” működik. Ha már meghatároztuk, hogy mennyi a “rossz” események aránya, akkor vegyük a “jó” eseményeket, azaz annak a valószínűségét, hogy “megfelel” a statisztikai modellünk. Ezt nevezzük konfidencia (megbízhatósági) szintnek. A definícióból következik, hogy ha szignifikancia szint \(\alpha\), akkor a konfidencia szint \(1-\alpha\). Még egy utolsó definícióra van szükségünk, a konfidencia intervallumra, amelybe azok az események (valószínűségi változók) tartoznak, amelyekre az összesített valószínűség megegyezik a konfidencia szinttel.

Legyen \(X_a,\,X_f\) a minta adataitól függő, két valószínűségi változó, amelyek a konfidencia intervallum alsó és felső határát adják. Célunk, hogy \(X_a,\,X_f\) értékeit úgy határozzuk meg, hogy \[ P(X_a < X < X_f)=1-\alpha \notag \]

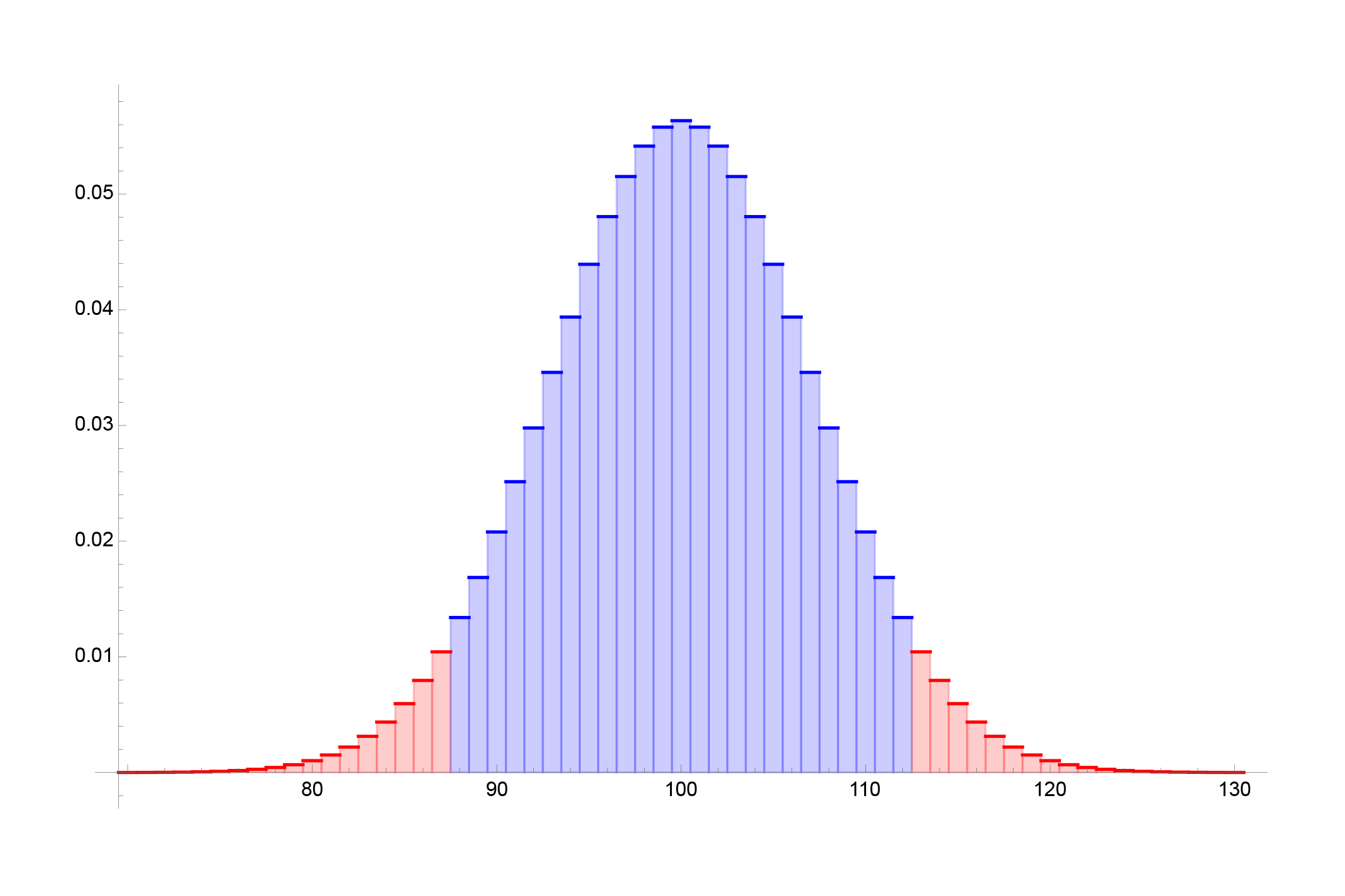
A fenti új fogalmakat próbáljuk megtölteni tartalommal, amely kapcsolódik a példánkhoz. Tekintsük a 200 pénzfeldobás eredményét, melyek binomiális eloszlást követnek. A pénzfeldobásokat többször elvégezzük egymás után, és felírjuk, hogy hány esetben volt fej és írás. Ha elégendően sokszor megismételjük, akkor a kapott eredményeket hisztogrammal ábrázolhatjuk, az \(x\) tengelyen legyenek 0-200-ig az értékek, hogy hány esetben volt a 200 pénzfeldobás közül pl. fej, az oszlopok magassága pedig azt mutatja meg, hogy a sokszor elvégzett kísérletek hány százalékában volt az adott, jelen esetben “fej” eredmény. A grafikon egy szimmetrikus alakzatot mutat, amely az elméleti eloszlást jeleníti meg. Ebben lehetnek kisebb-nagyobb torzulások, ha valós pénzfeldobást vizsgálunk.

Ez eddig meglehetősen száraz volt és sok újdonságot tartalmazhatott, de most térjünk át az eredetileg vizsgálandó problémánkhoz, és értelmezzük ennek alapján a fentieket. Látjuk a hisztogramból, és tapasztalati úton is tudjuk, hogy annak a valószínűsége, hogy 200 pénzfeldobásból mind fej, vagy mind írás elenyésző (az első hisztogram 70, az utolsó pedig 130 esetet jelöl, amikor az eredmény fej volt). Kiemelkedő annak a valószínűsége, hogy 100-szor fej és 100-szor írás az eredmény, összhangban a várakozásainkkal – a középső legmagasabb oszlop. Talán újdonság lehet, hogy annak a valószínűsége, hogy 50-50%-ban lesz fej vagy írás az eredmény, meglehetősen alacsony, alig haladja meg az 5%-ot.

Az utolsó megállapításból egy fontos következtetést vonhatunk le, ha egy kissé átfogalmazzuk. Ha több mintát vizsgálunk, akkor az 50-50%-os eredményt csak az esetek 5%-ban várjunk el, azaz meglehetősen ritka esemény. Ez azonnal egy figyelmeztető jel lehet egy adatsor elemzésénél, főleg akkor, ha ezt a mérést rendszeresen elvégezzük és az esetek többségében pont az 50-50%-os eredményt kapjuk.

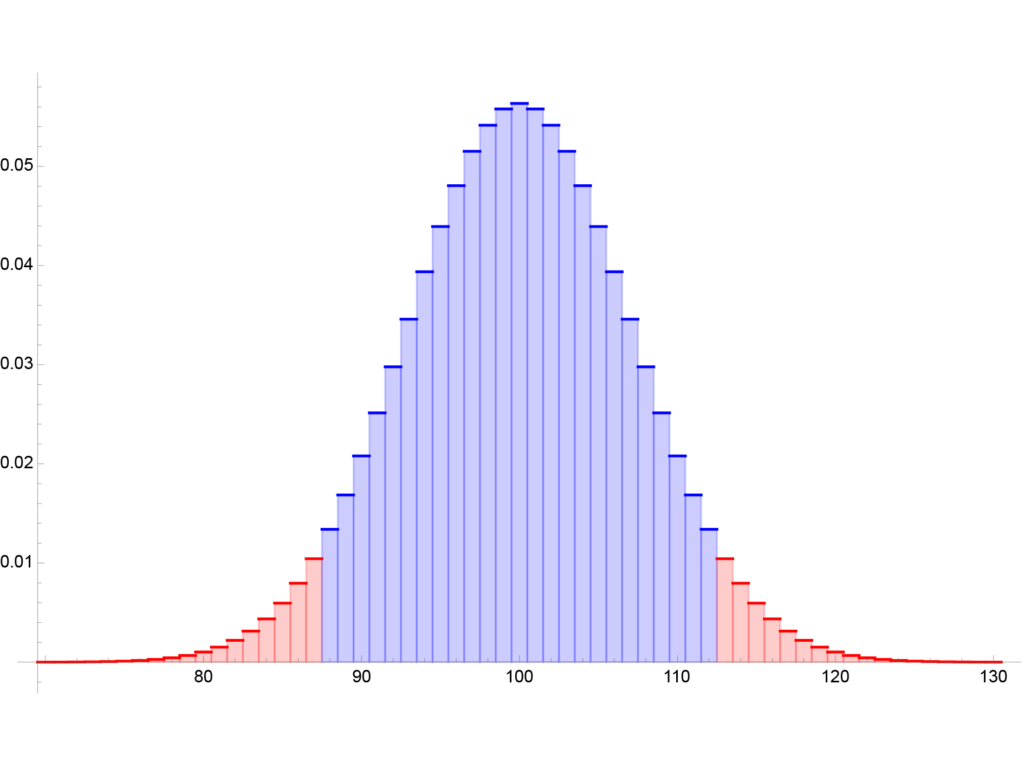Hogyan tudnánk egy módszert kapni arra vonatkozóan, hogy az eredmény “reális”, statisztikailag elfogadható? Használjuk fel az előzőekben megismert fogalmakat és elvet. Legyen a szignifikancia szint 10%, és keressük meg a konfidencia intervallumot! Ezt érdemes lefordítani. Azokat a fej-írás arányokat keressük, amelyek az esetek többségében, azaz azok 90%-ban előfordul (\(1-0,1\)). Ezt tekintjük “jó” eseményeknek, azaz esetünkben “hihető” szabályos érmével végzett kísérletnek. Az ábráról könnyel leolvashatjuk, a szimmetria miatt, hogy a 100-as értéktől jobbra és balra szimmetrikusan kell keresnünk a “jó” és a “rossz” eseményeket is. A részletes számítást most nem vesszük végig, de az eredmény magáért beszél.

Ha a kékkel jelölt oszlopok magasságát összeadjuk, akkor az egyes kimenetekhez tartozó valószínűségeket összegeztük, amelyre az elvár (minimum) érték 90%, a feltételezésünk szerint – ez a konfidencia szint. Ebből már könnyen meghatározható a konfidencia tartomány, azaz milyen arányokat kapunk nagy (minimum 90%-os) valószínűséggel. Ha azoknak az eseteknek a valószínűségét összegezzük, amikor 88-112 között van a fej dobások száma a 200-ból, akkor elérjük a kívánt szintet, azaz a konfidencia intervallum \([88,\,112]\). Fordítsuk meg a gondolatmenetet, annak a valószínűsége, hogy a 200 pénzfeldobás esetén \(0,\,1,\,2,\,\ldots,\,87\) valamelyike a fejdobások száma, azaz 200 dobásból, 0 vagy 1 vagy 2 vagy… a fej érték), nem több mint 5% – összesen. Ugyanez mondható el a jobb oldali 113-200-as tartományra is. Így a konfidencia intervallumon kívüli események összes valószínűsége 10%.

Az oldal tetején található véletlenszerű 0-1 sorban 102 darab 1-es és 98 darab 0 van. Véletlenszám generátorral megnéztünk további 5 esetet és a következő eredményt kaptuk az 1-ek számára: 111, 108, 101, 96, 103. Az előzőek fényében nem véletlen, hogy a 100-as eredmény nem jött ki, csak 5% volt az esélye.

Az első figyelmeztető jel az adatok manipuláltságára az, ha az “elméleti valószínűséget” kapjuk eredményül. Főleg abban az esetben, ha több mintában is ezt tapasztaljuk. Az eredmény manipulációra utal annak ellenére, hogy “azt kapjuk, amit várunk”.

Tehát ha egy osztályban megkérjük a tanulókat, hogy írják fel a 200 pénzfeldobás eredményét, akkor az a leggyanúsabb, hogy nem pénzfeldobás alapján írta fel az eredményeket, akinél a fejek és írások száma egyenlő.