| Ponthalmaz egyenlete | Megjegyzés | Ábra |
|---|---|---|
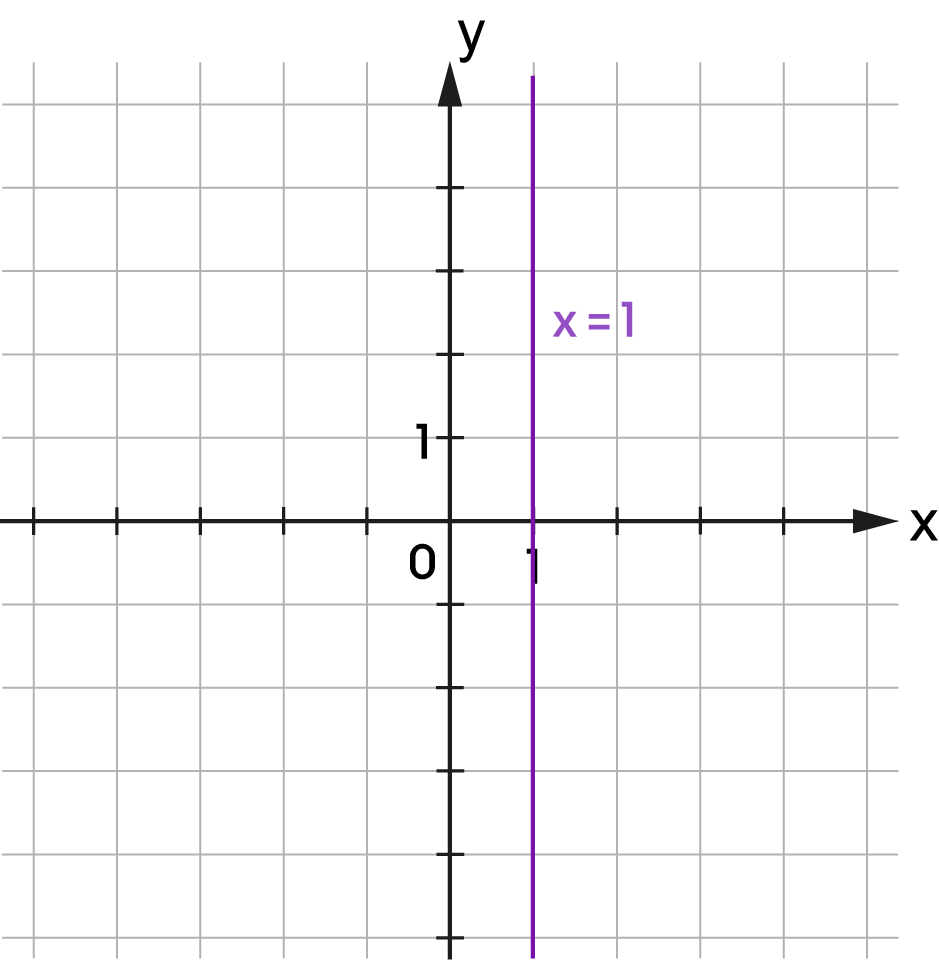
| \(x=1\) |
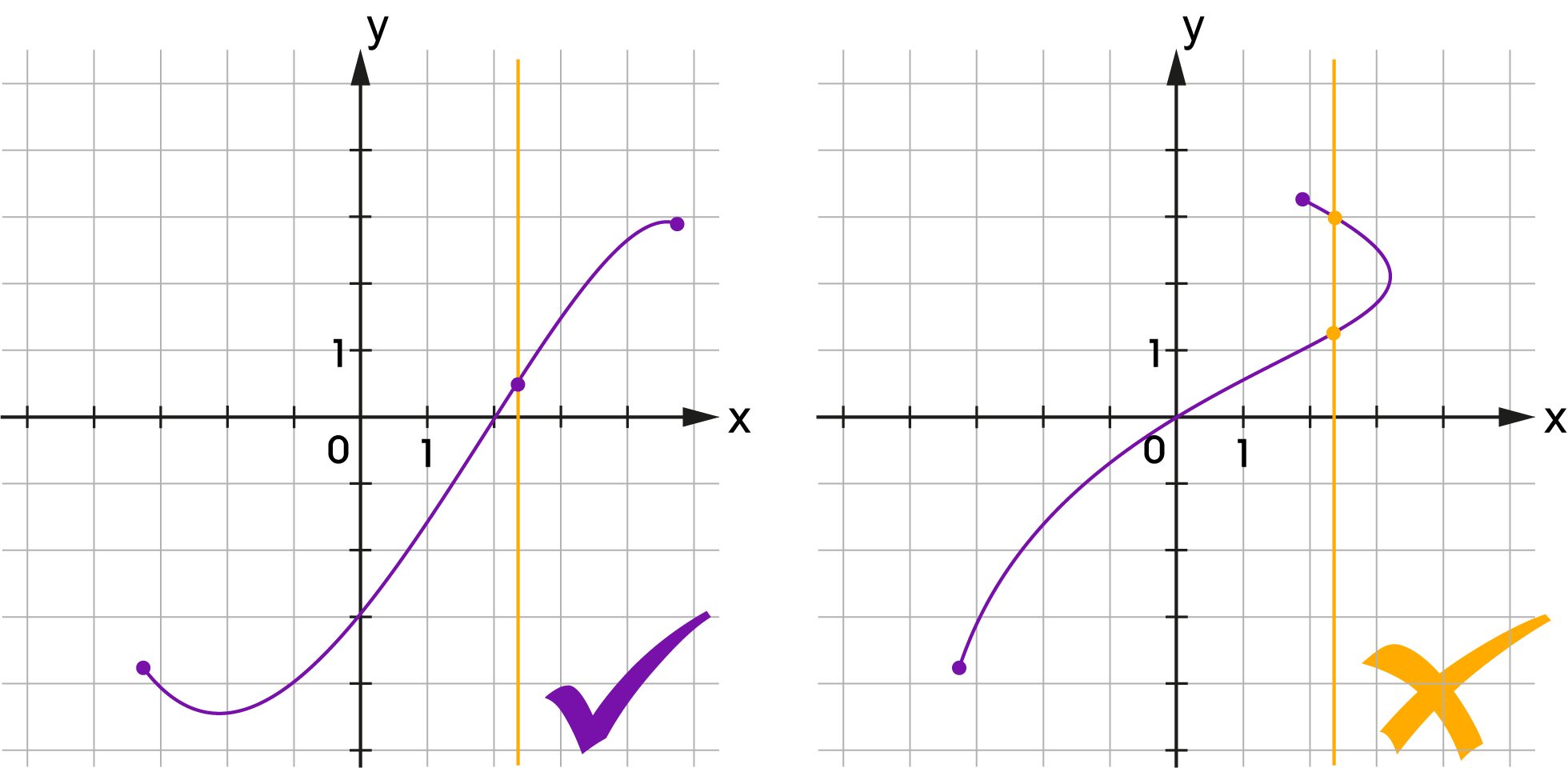
A ponthalmaz nem függvény.
Az \(x=c\) egyenlettel megadott ponthalmazok nem függvények , ahol \(c\in\mathbb{R}\). |
 |
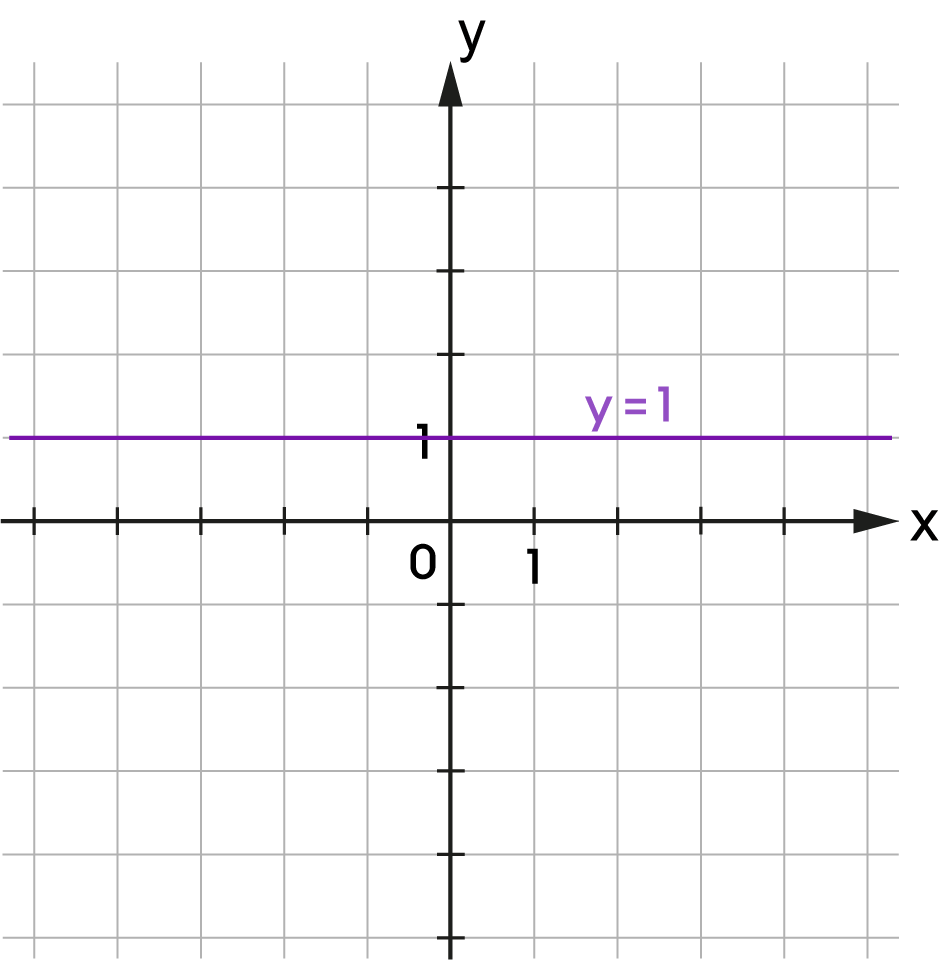
| \(y=1\) |
A ponthalmaz függvény.
Az \(y=c\) egyenlettel megadott ponthalmazok függvények, ahol \(c\in\mathbb{R}\). |
 |
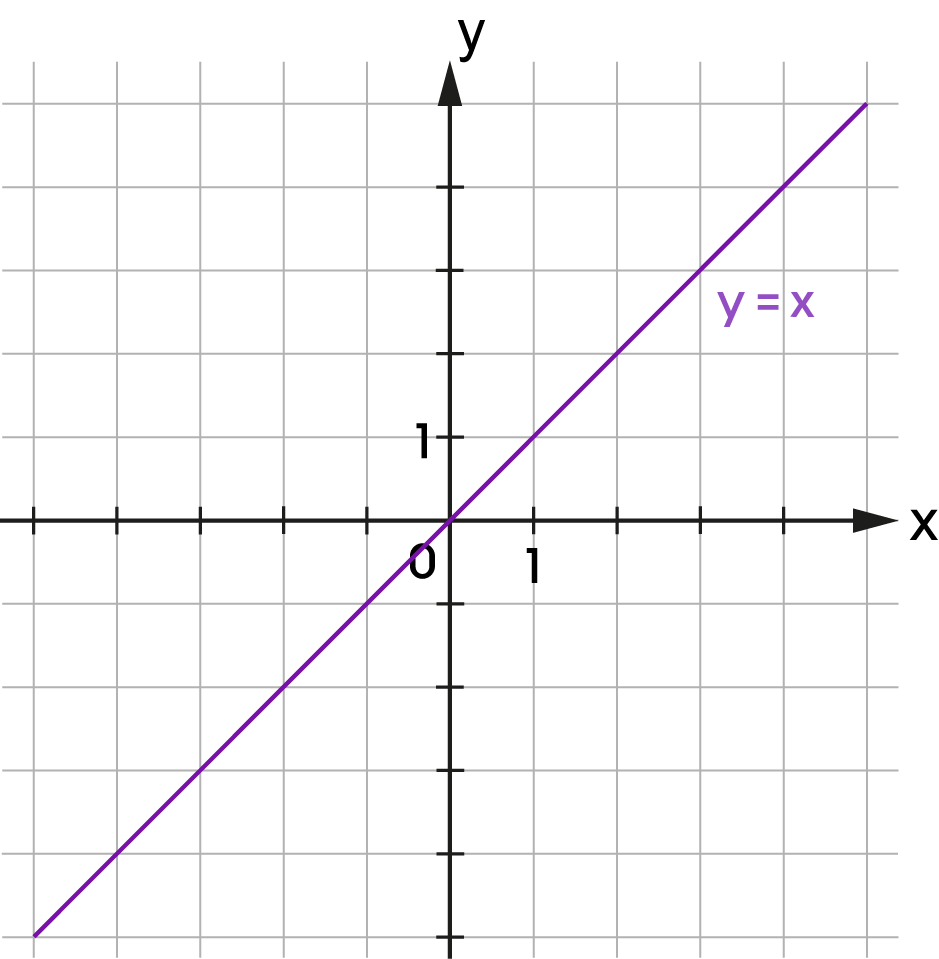
| \(y=x\) |
A ponthalmaz függvény.
Az \(y=x\) egyenlettel megadott ponthalmaz, azon pontok halmaza, amelyekre teljesül, hogy az első és a második koordinátájuk megegyezik. |
 |
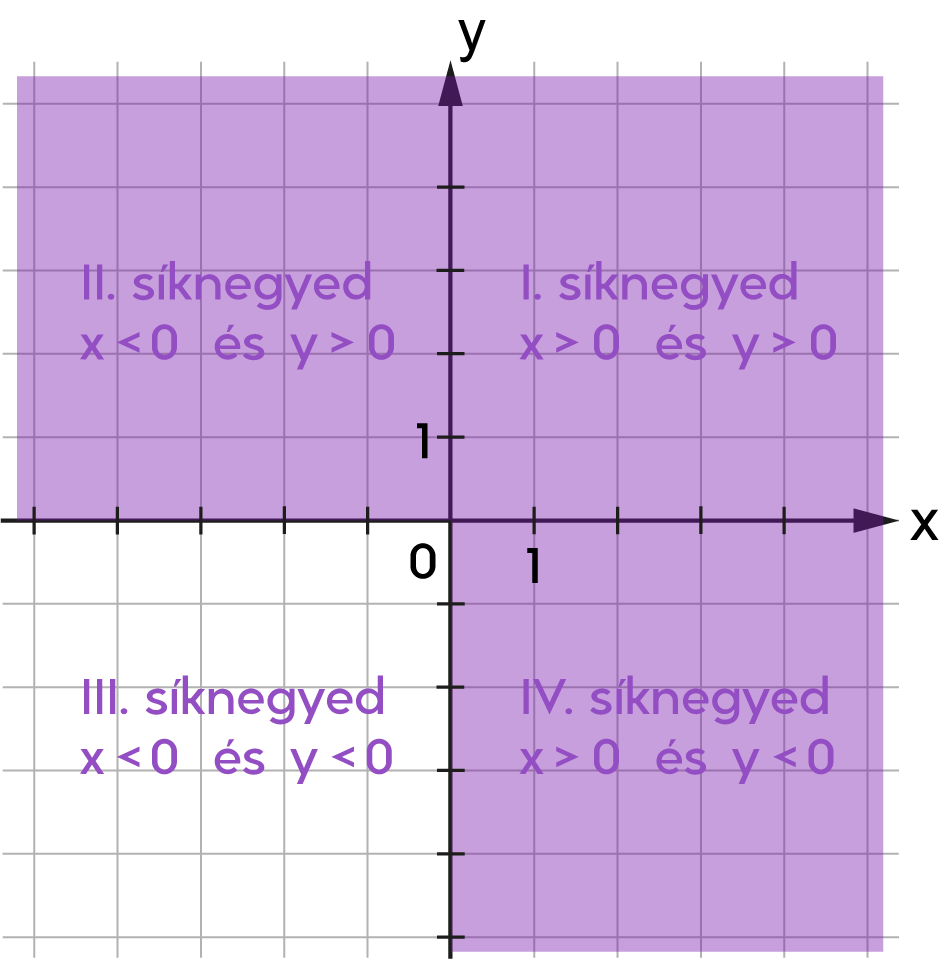
| \(x > 0\) vagy \(y > 0\) |
A ponthalmaz nem függvény.
Az ábrán az egyes síknegyedeket is jelöljük a koordináta-rendszerben. |
 |
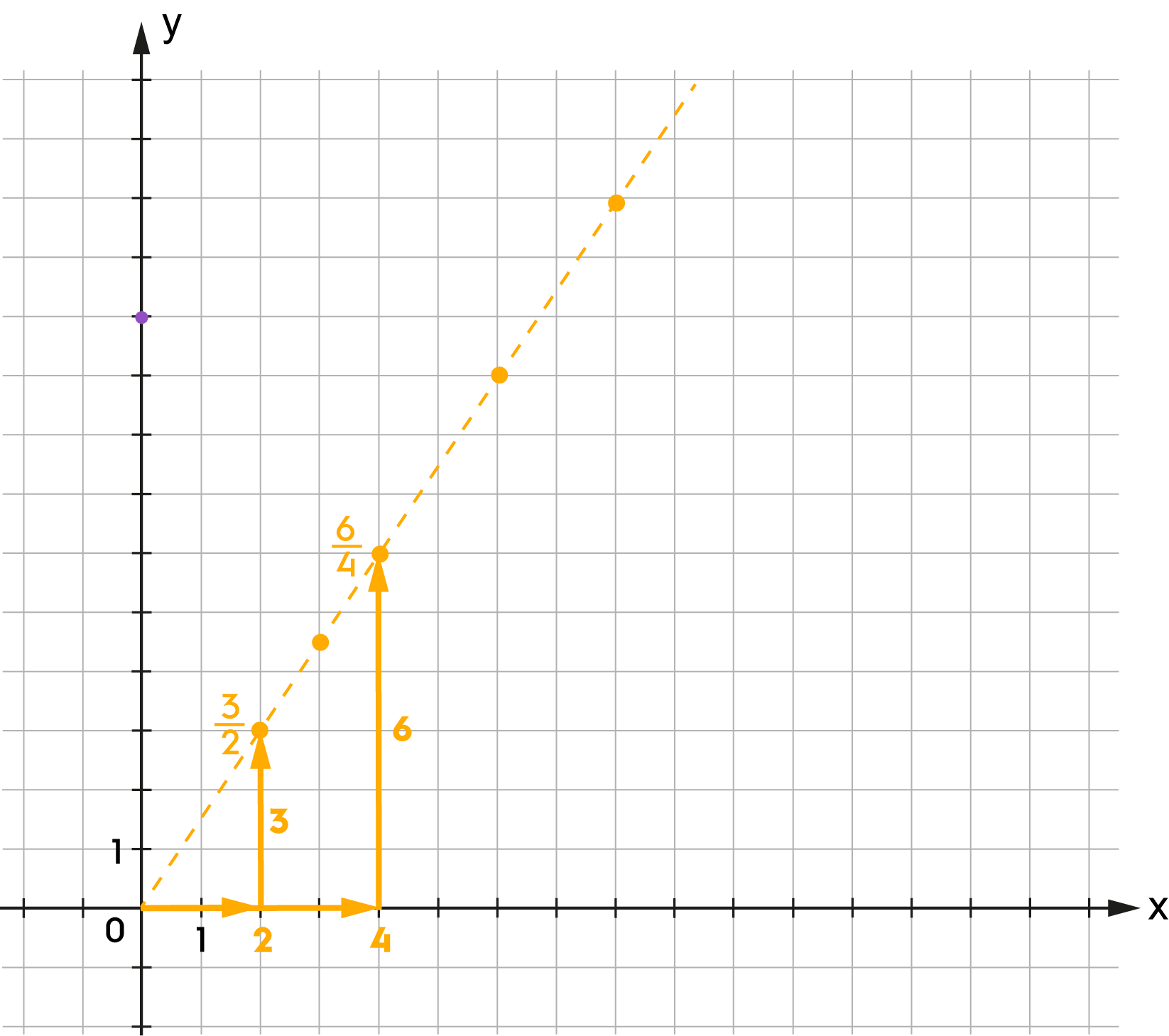
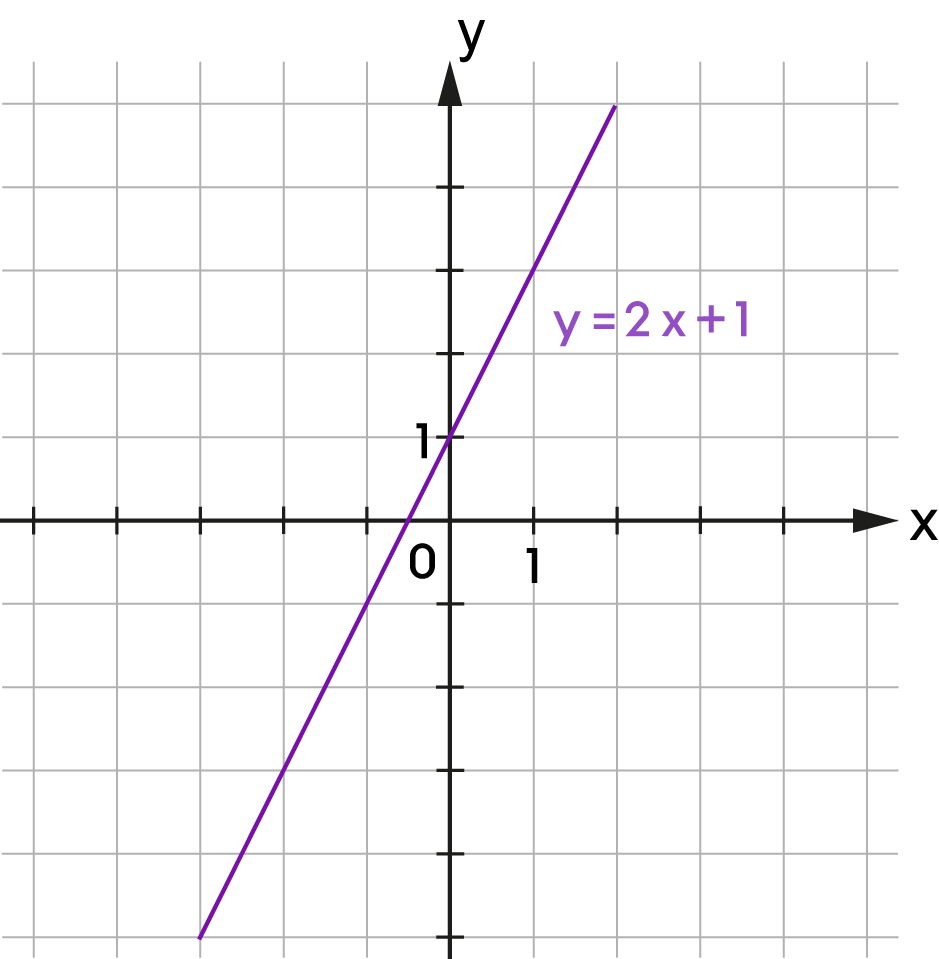
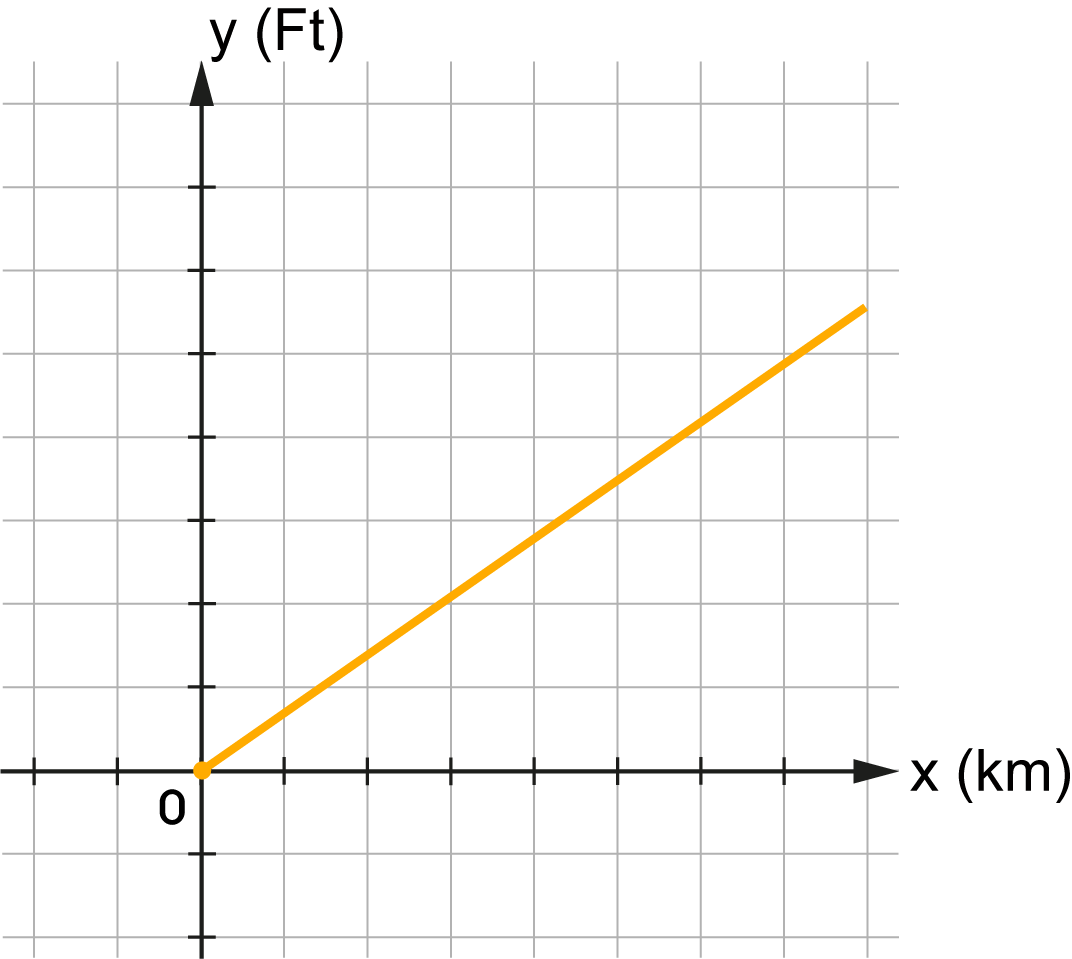
| \(y = 2x+1\) |
A ponthalmaz függvény.
Az \(y=ax+b\) egyenlettel meghatározott ponthalmaz egy egyenes, ahol \(a,\,b\in\mathbb{R}\). Ha \(b=0\), akkor az egyenes áthalad a koordináta-rendszer origóján, és pontjainak koordinátái egyenes arányosságban állnak. |
 |
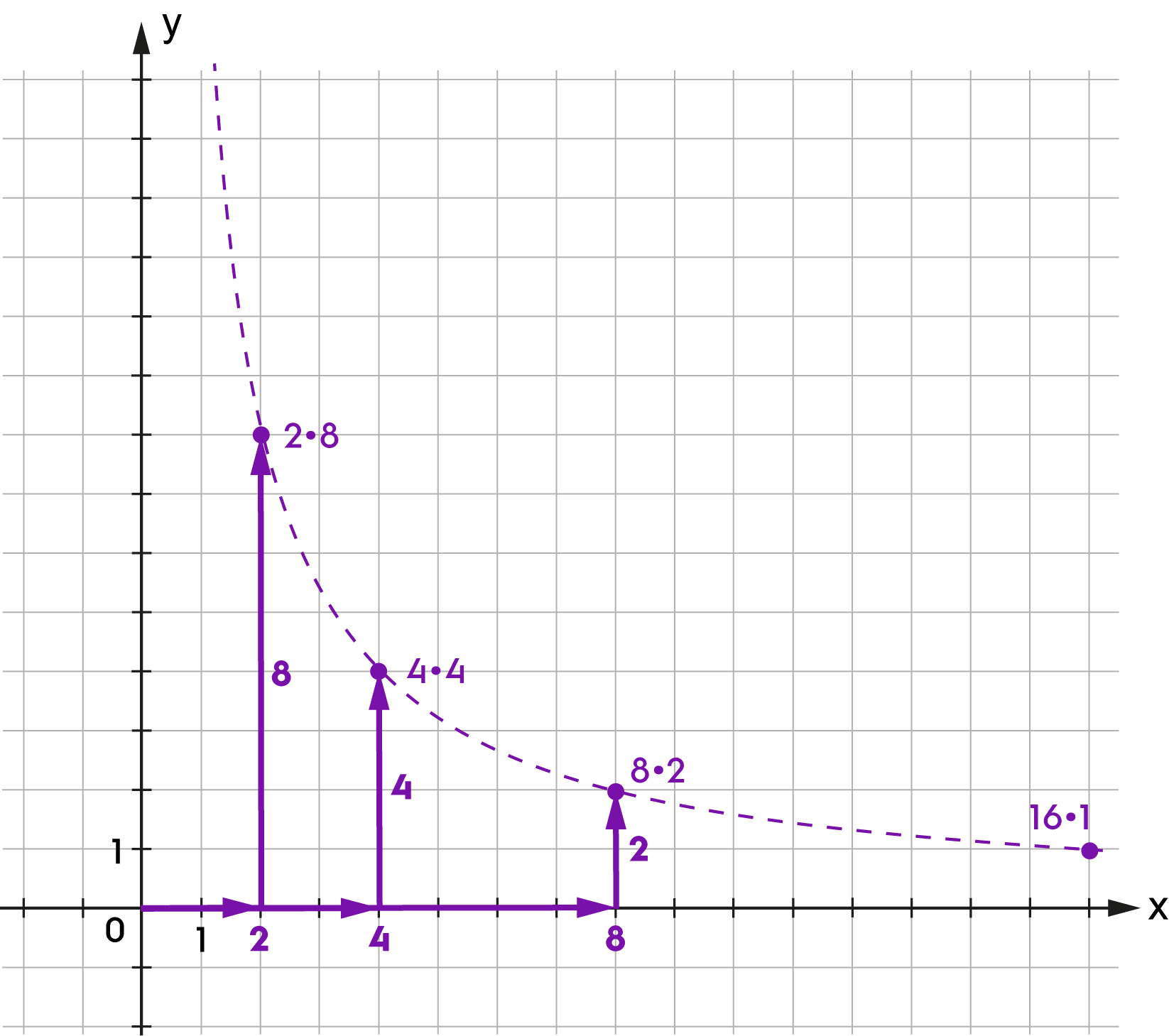
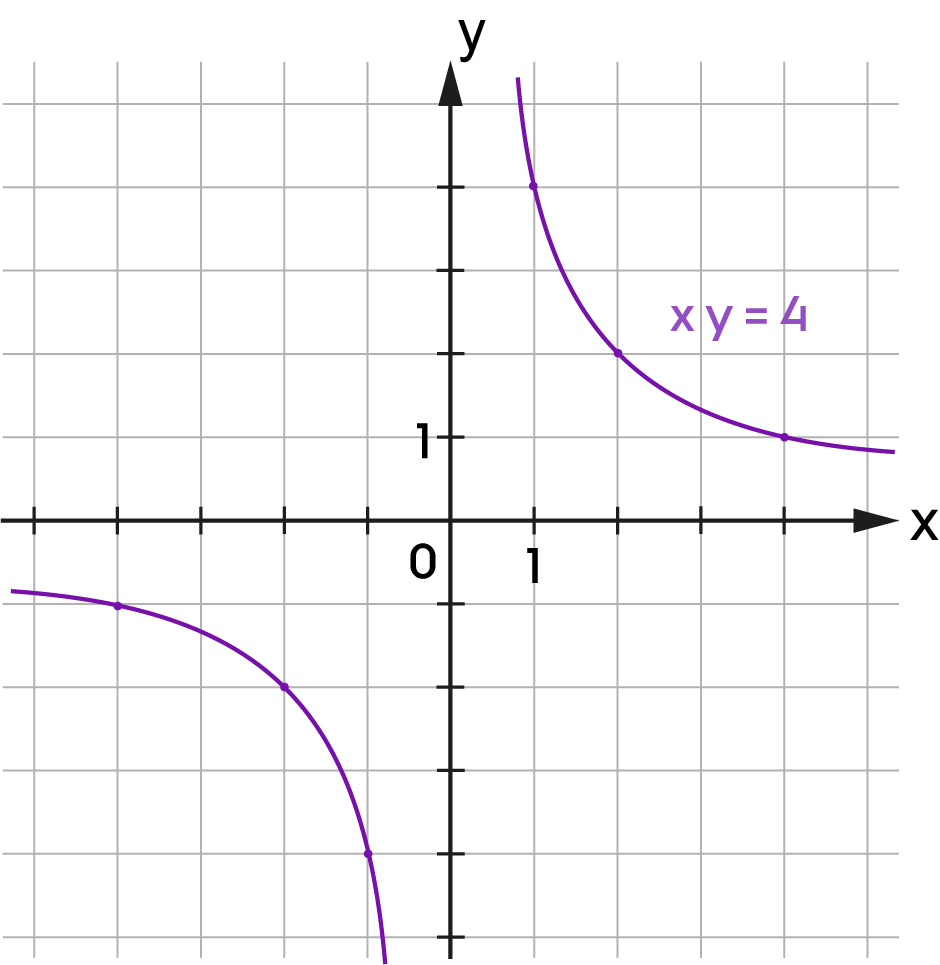
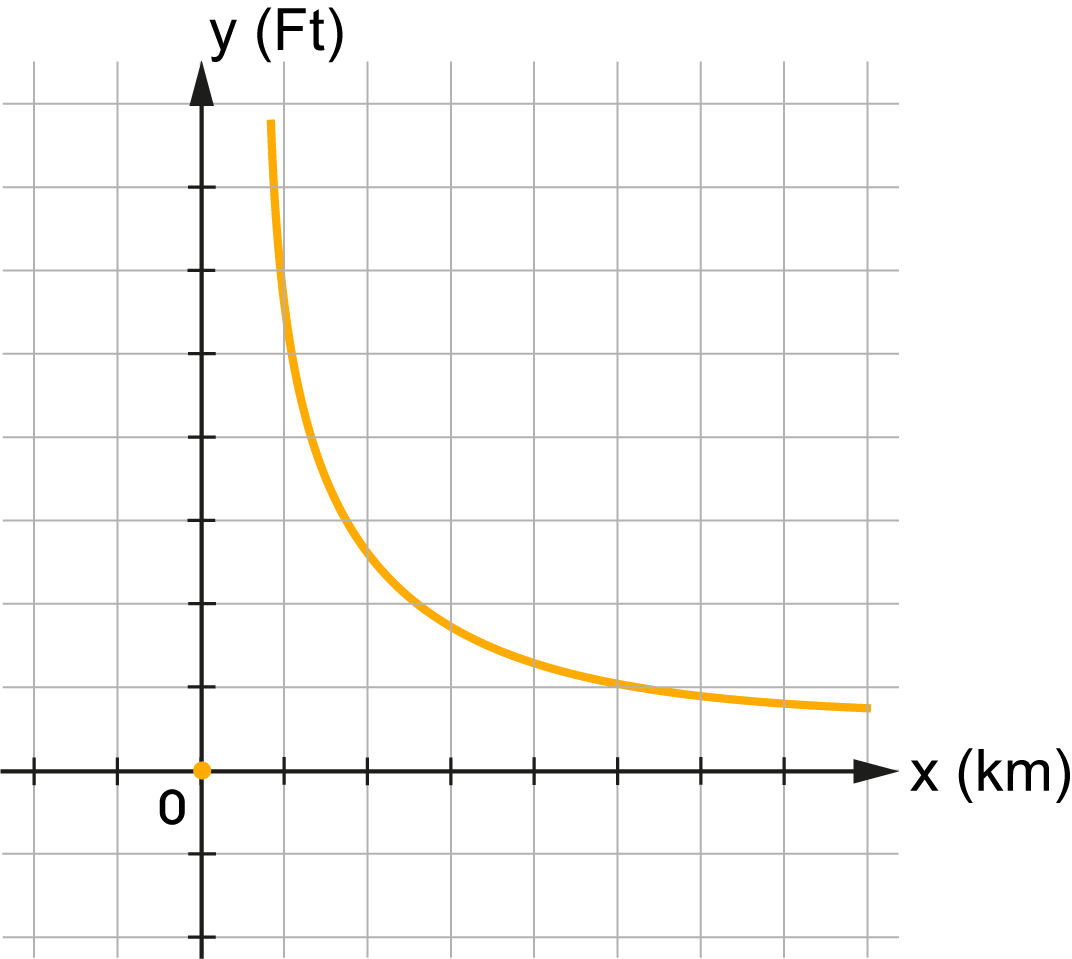
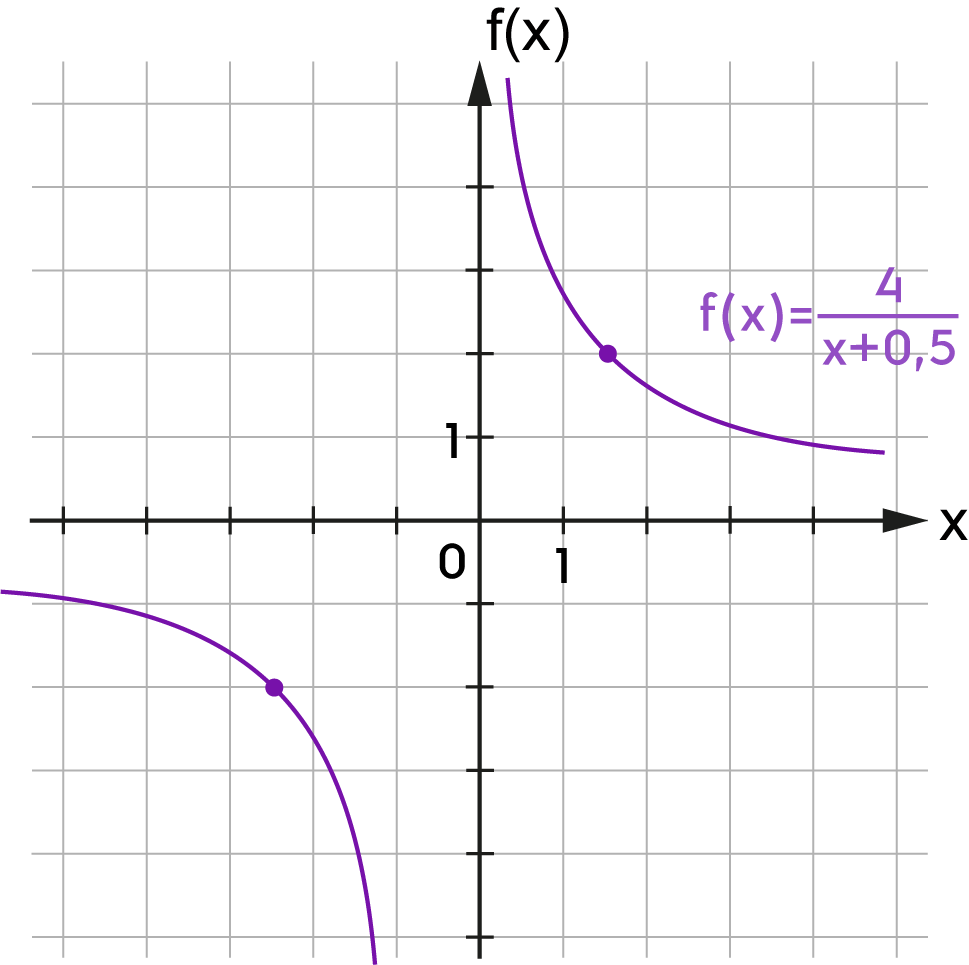
| \(xy = 4\) |
A ponthalmaz függvény.
Az \(xy=c\) egyenlettel meghatározott ponthalmaz egy hiperbola, ahol \(c\in\mathbb{R}\). Az egyenlet által meghatározott ponthalmaznak nem eleme az \(O(0;0)\) pont, és pontjainak koordinátái fordított arányosságban állnak. |
 |
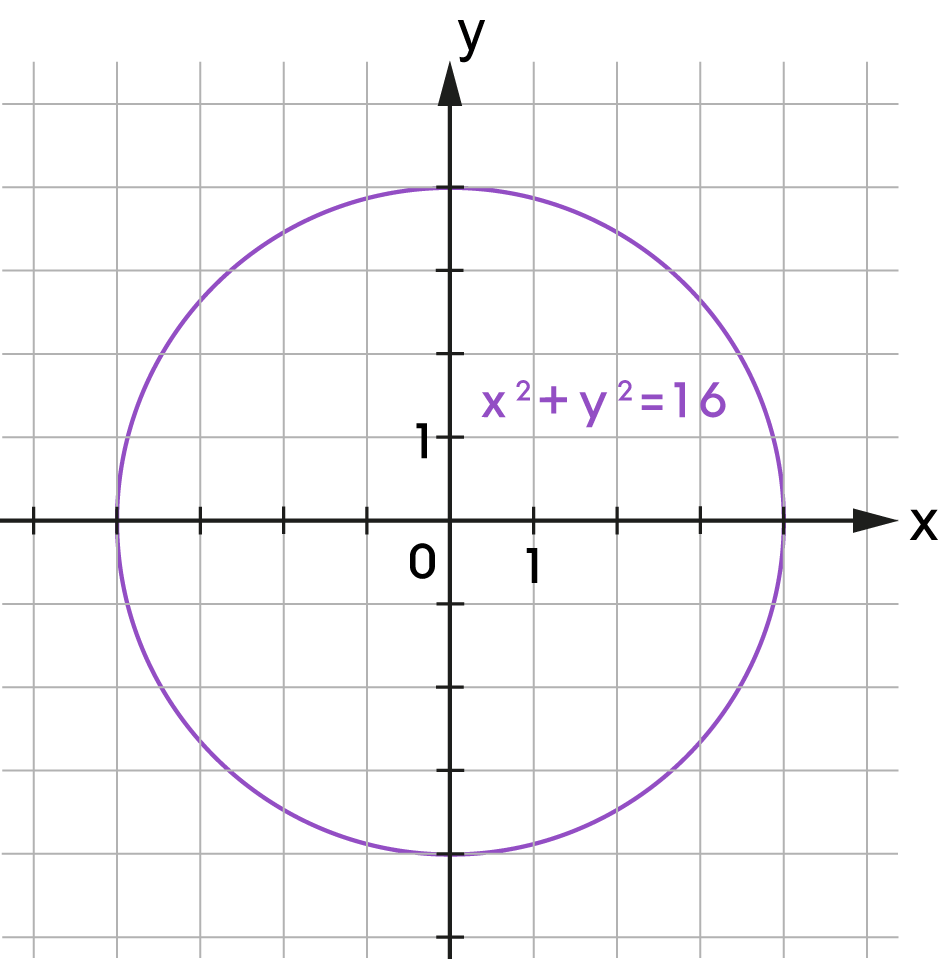
| \(x^2+y^2 = 16\) |
A ponthalmaz nem függvény.
Az \(x^2+y^2=c\) egyenlettel meghatározott ponthalmaz egy kör, ahol \(c\in\mathbb{R}\) és a kör sugara \(\sqrt c\). A kör középpontja az \(O(0;0)\) pont. |
 |
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
 |
|
 |
|
 |
|
 |
|

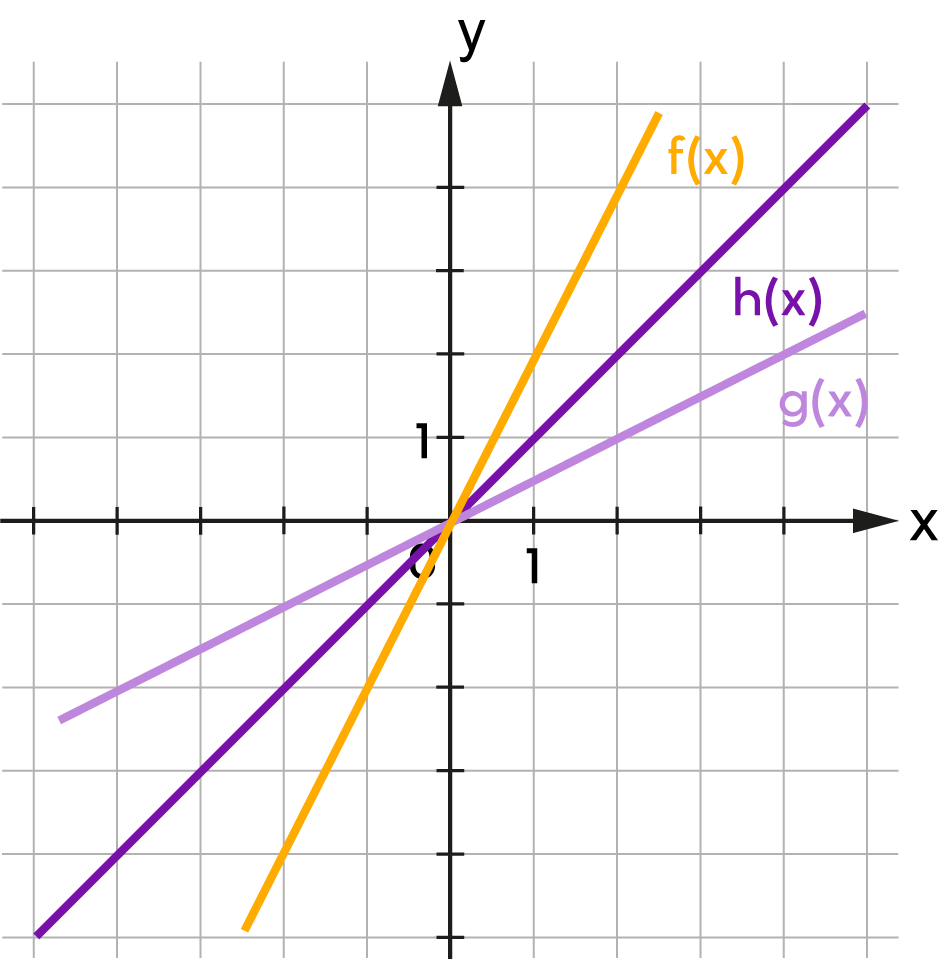
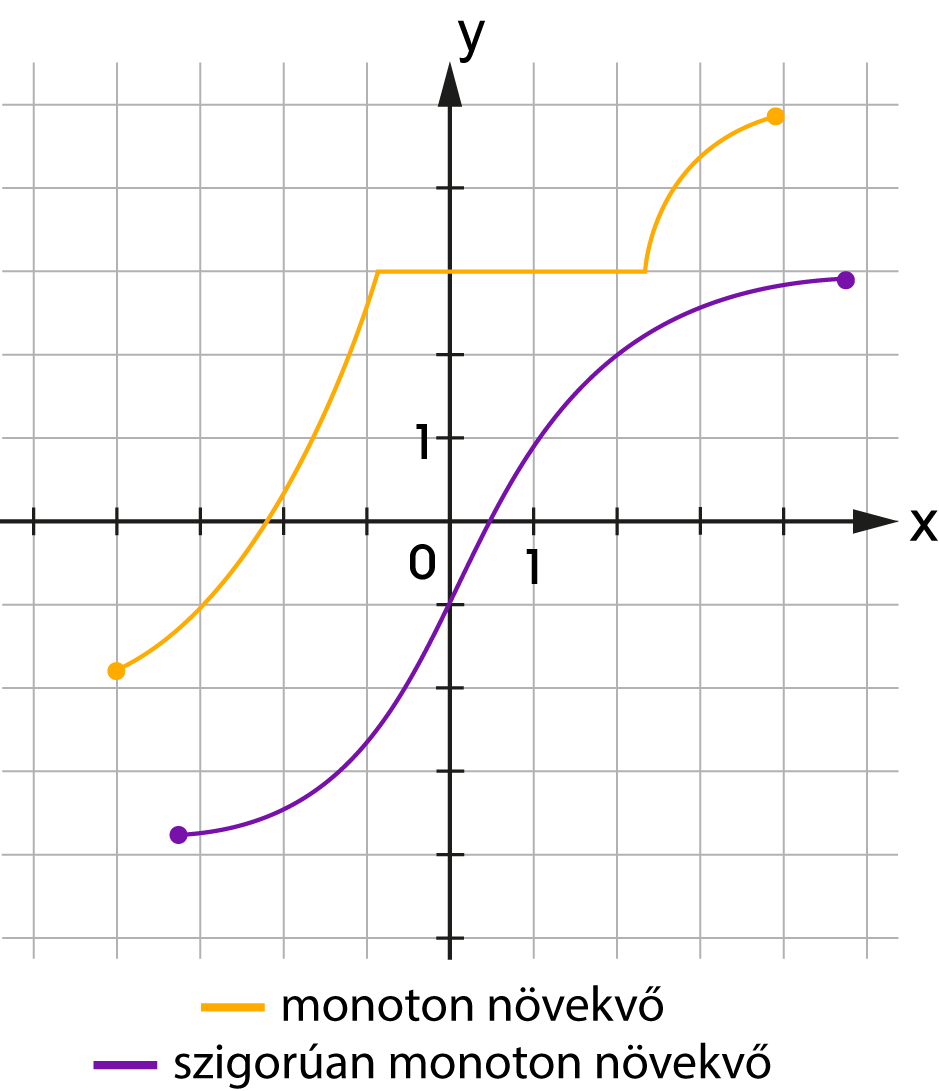 Az \(f\) függvényt az értelmezési tartományának egy \(I\) intervallumán \(I\in D_f\) szigorúan monoton növekvőnek (ill. csökkenőnek) nevezzük, ha \(I\) minden \(x_1 < x_2\) elemei esetén teljesül, hogy \(f(x_1) < f(x_2)\) \(\big(\text{ill.}\,f(x_1) > f(x_2)\big)\).
Az \(f\) függvényt az értelmezési tartományának egy \(I\) intervallumán \(I\in D_f\) szigorúan monoton növekvőnek (ill. csökkenőnek) nevezzük, ha \(I\) minden \(x_1 < x_2\) elemei esetén teljesül, hogy \(f(x_1) < f(x_2)\) \(\big(\text{ill.}\,f(x_1) > f(x_2)\big)\).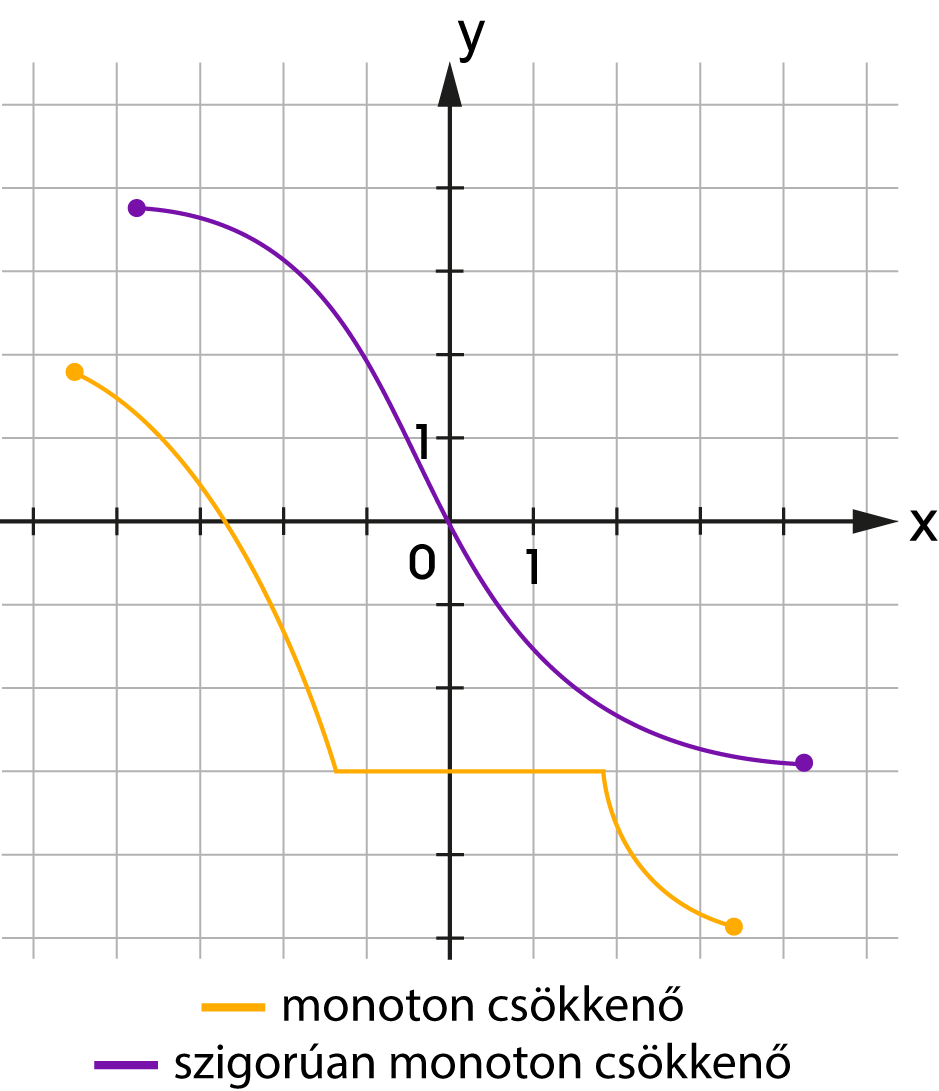
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
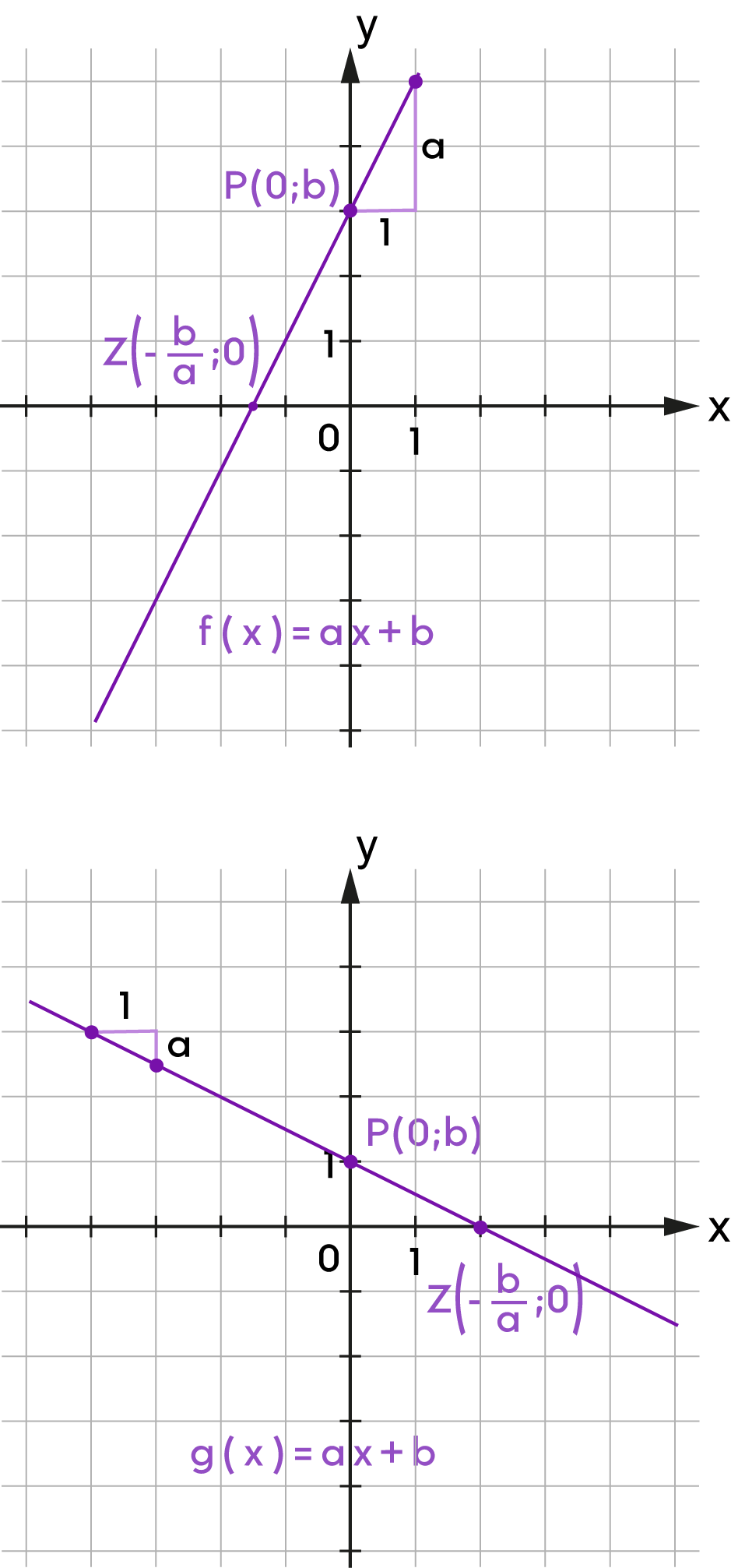
Az eredményeket közönséges tört alakban add meg, amelyben a számláló és a nevező relatív prímek!
| A függvény meredeksége: \(-\) | ||
| A függvény zérushelye: | ||
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
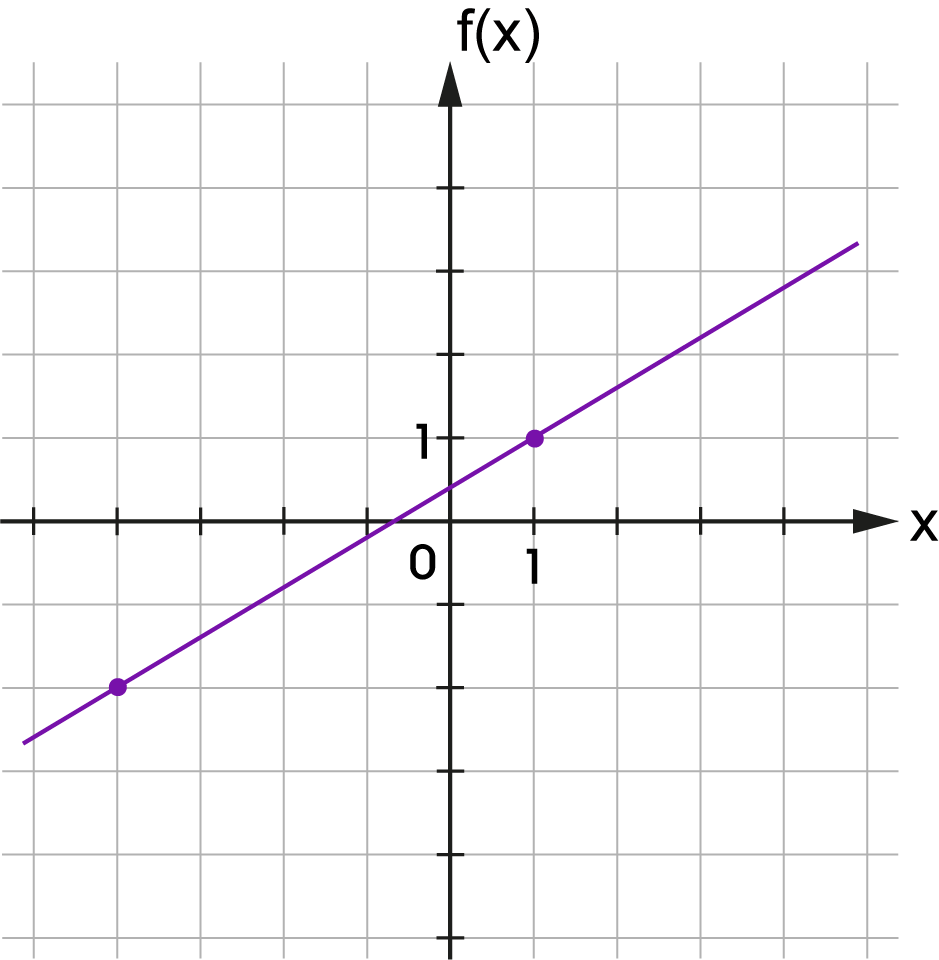
Az eredményeket közönséges tört alakban add meg, amelyben a számláló és a nevező relatív prímek!
| \(f(x)=\) | \(\,x\;+\) | |||
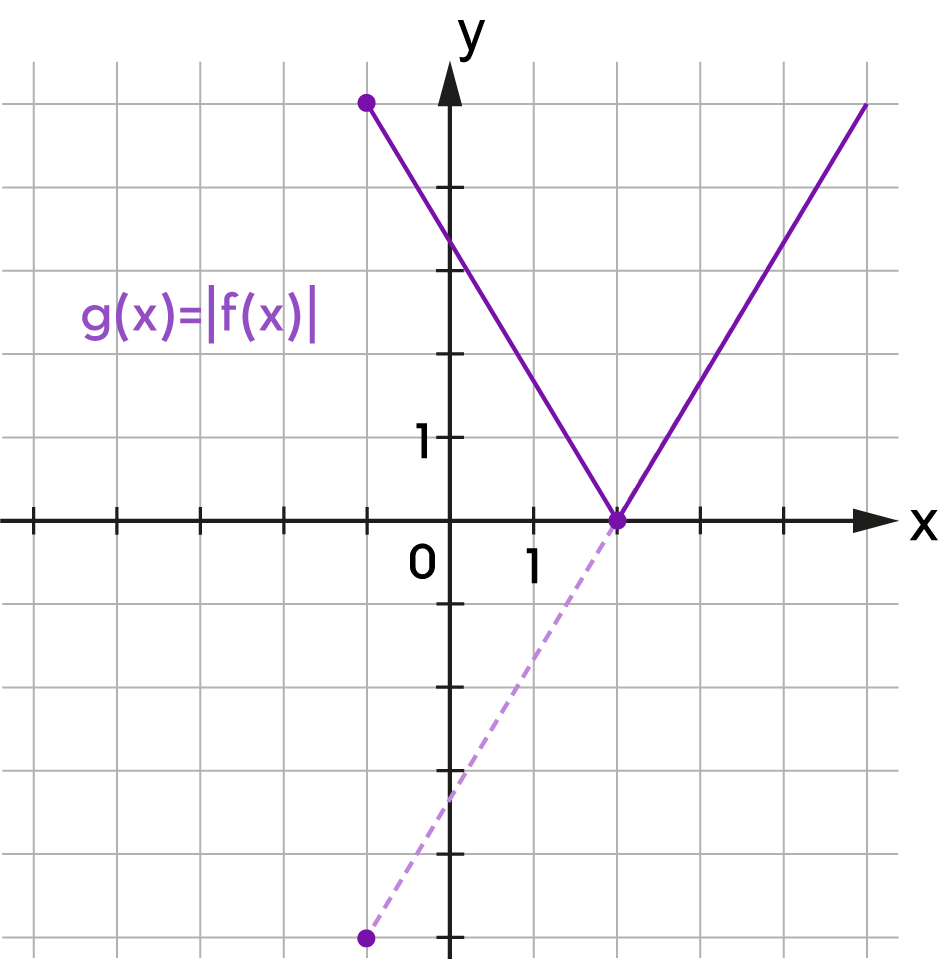
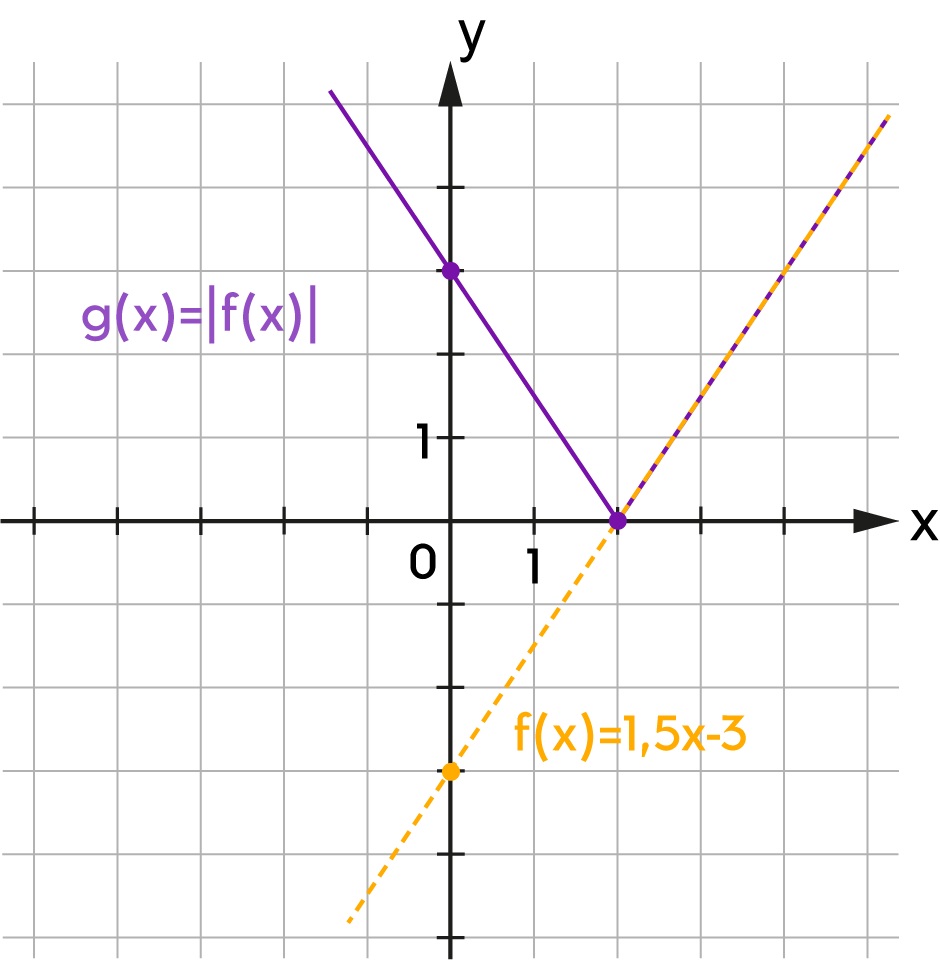
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
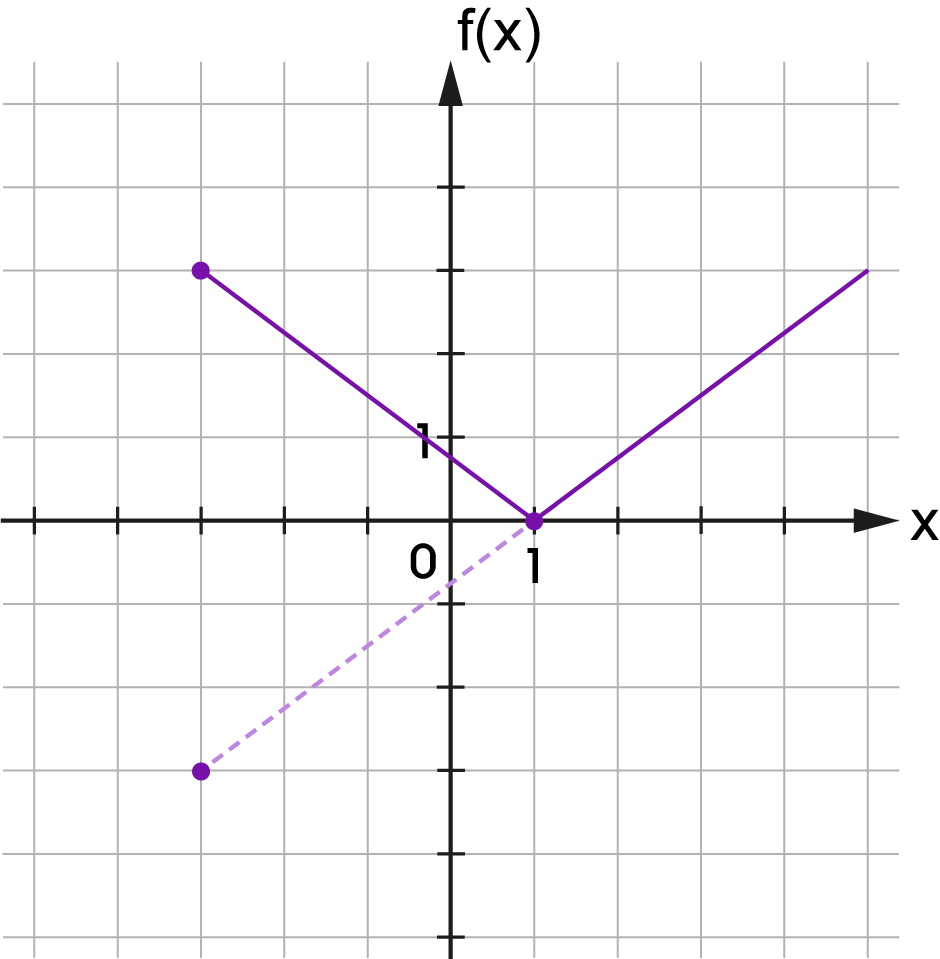
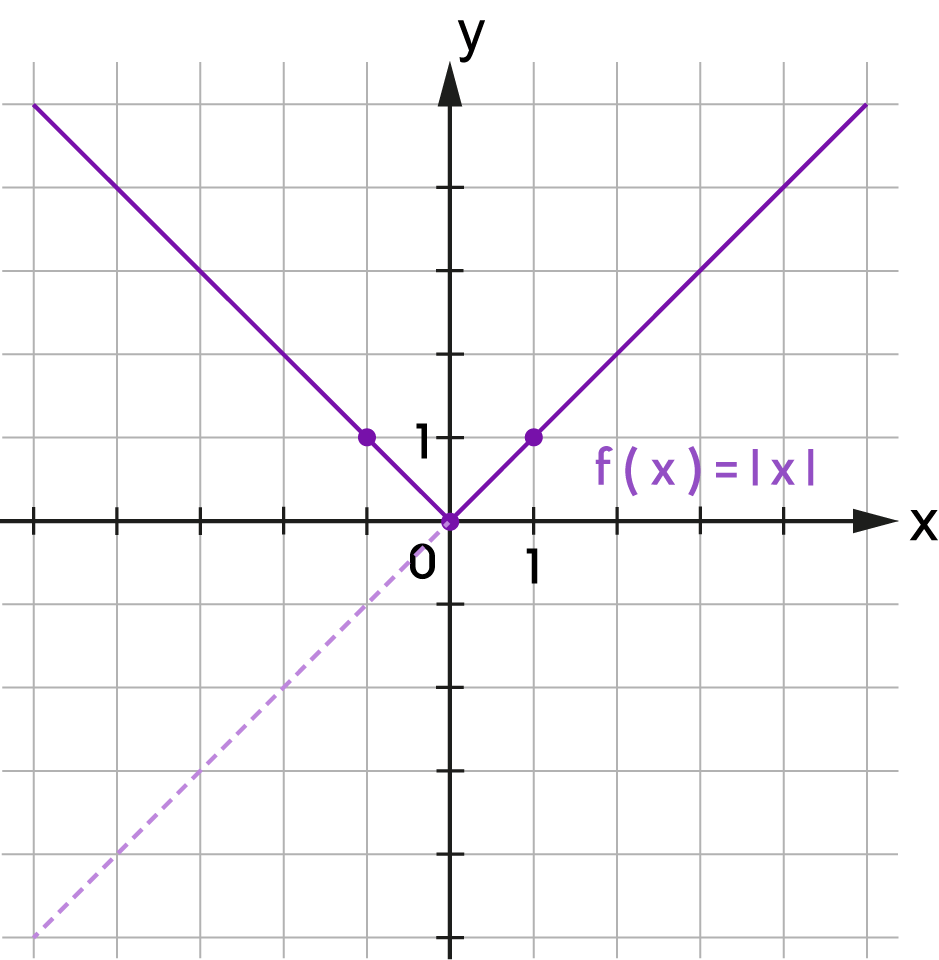
Az eredményeket közönséges tört alakban add meg, amelyben a számláló és a nevező relatív prímek!
| \(f(x)=\) | \(\,x\;-\) | |||||
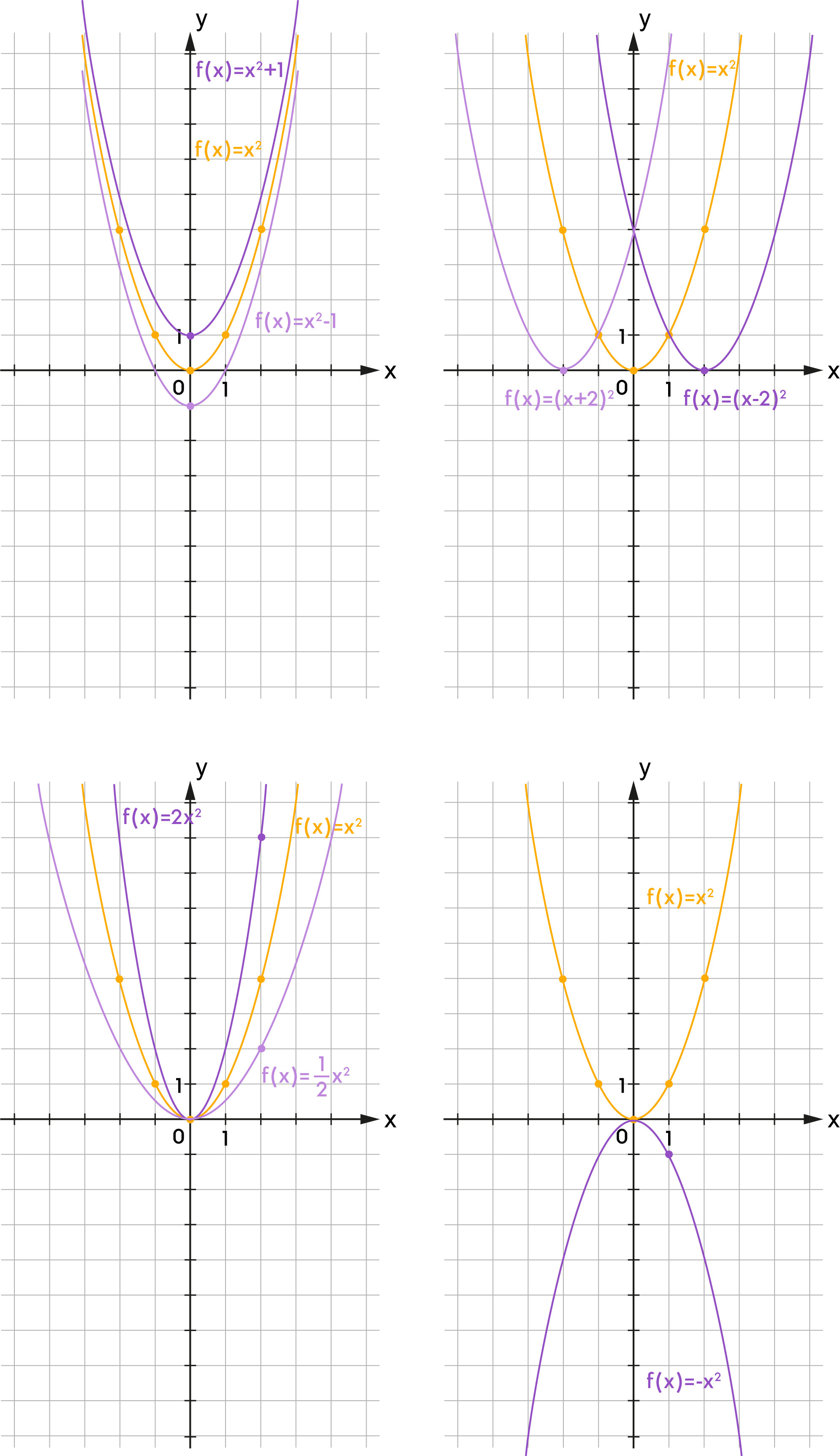
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
1 kérdésből 0 befejezve
Kérdések (a kérdés számára klikkelve folytathatod a megoldást):
Korábban már befejezted a feladatsor-t. Emiatt nem kezdheted újra.
Feladatsor töltődik...
Be kell jelentkezned vagy regisztrálnod kell, hogy elindítsd ezt a feladatsort
Előbb be kell fejezned a következőt:
A megadott idő lejárt
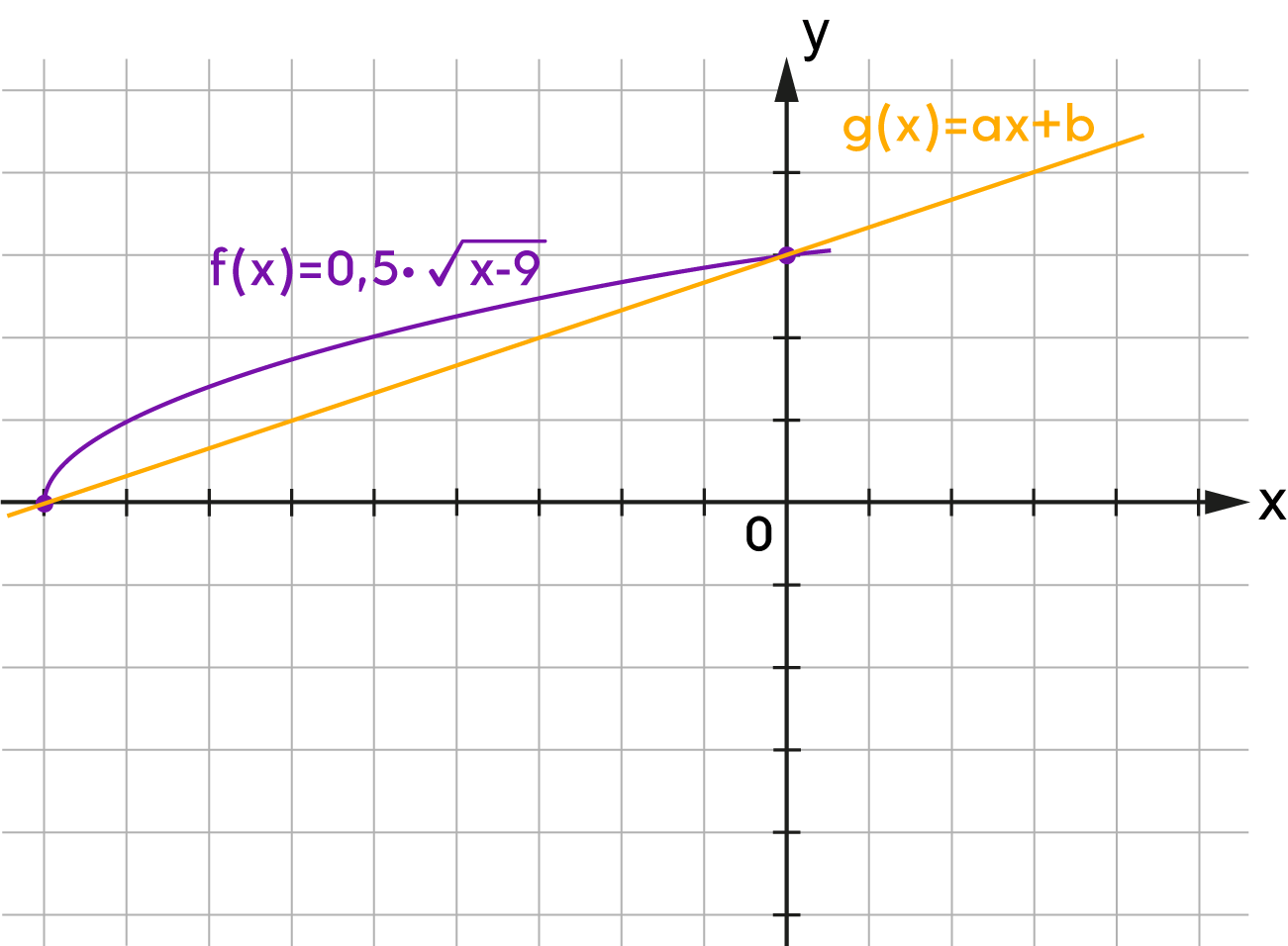
| Az \(f(x)\) függvény tengelymetszeti pontjaira illeszkedő egyenes egyenlete \(g(x)=\) | \(\,x\;+\) | |||
 Copyright © iMatek 2020-2025 – Minden jog fenntartva
Copyright © iMatek 2020-2025 – Minden jog fenntartva