iMatek

Elmélet minta – Hatványközepek közötti egyenlőtlenség

iKurzusok
iFeladatok

Bemutató – Emelt szintű érettségi online felkészítő Minta fejezet – Szélsőérték feladatok Elmélet minta – Hatványközepek közötti egyenlőtlenség
\(\pmb{Definíció:}\)
Legyenek \(a_1,\,a_2,\ldots,\,a_n\) nemnegatív valós számok és \(k \neq 0\), akkor \(a_1,\,a_2,\ldots,\,a_n\) számok \(k\)-dik hatványközepe: \[ S_k(a_1,\,a_2,\ldots,\,a_n)=\left(\sum_{i=1}^n \frac{a_i^k}{n}\right)^\frac{1}{k} \notag \] \(k=0\) esetén a hatványközepet a következő módon definiáljuk: \[ S_0(a_1,\,a_2,\ldots,\,a_n)=\sqrt[k] {a_1\cdot a_2\cdot\ldots\cdot a_n} \notag \]
\(\pmb{Tétel:}\)
A hatványközepek közötti egyenlőtlenség szerint, ha \(a_1,\,a_2,\ldots,\,a_n\) nemnegatív valós számok, akkor \(p < q\) \[ S_p\leq S_q \notag \]
\(\pmb{Megjegyzés:}\)
\[ \begin{aligned} S_{-1}(a_1,\,a_2,\ldots,\,a_n)&=H_n=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}}& \text{ harmonikus közép}\\ \end{aligned}\notag \]
\[ \begin{aligned} S_{0} (a_1,\,a_2,\ldots,\,a_n)&=M_n=\sqrt[n]{a_1\cdot a_2\cdot\ldots\cdot a_n}& \text{ mértani közép}\\ \end{aligned}\notag \]
\[ \begin{aligned} S_{1} (a_1,\,a_2,\ldots,\,a_n)&=A_n=\frac{a_1+a_2+\ldots +a_n}{n}& \text{ számtani közép}\\ \end{aligned}\notag \]
\[ \begin{aligned} S_{2} (a_1,\,a_2,\ldots,\,a_n)&=Q_n=\sqrt{\frac{a_1^2+a_2^2+\ldots +a_n^2}{n}}& \text{ négyzetes közép}\\ \end{aligned}\notag \]
\(\pmb{Megjegyzés:}\)
A fenti nevezetes középértékeket szemléltethetjük is egy trapéz segítségével.
A trapéz szárainak \(F_1,\,F_2\) felezőpontjait összekötő \(x\) hosszúságú szakasz az alapok hosszúságának a számtani közepe. \[ x=\frac{a+b}{2}\notag \]
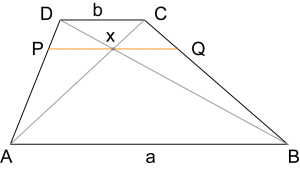A trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos \(x\) szakasz hossza az alapok harmonikus középe.
\[
x=\frac{2}{\frac{1}{a}+\frac{1}{b}}\notag
\]
Ha a trapézt hasonló trapézokra vágjuk egy \(\overline{PQ}\) szakasszal, amely párhuzamos az alapokkal, azaz \(\dfrac{a}{b}=\dfrac{m_2}{m_1}\), akkor az \(x=\overline{PQ}\) szakasz hossza az alapok mértani közepe. \[ x=\sqrt{a\cdot b}\notag \]
Ha a trapézt egyenlő területű trapézokra osztjuk egy \(\overline{PQ}\) szakasszal, amely párhuzamos az alapokkal, akkor az \(x=\overline{PQ}\) szakasz hossza az alapok négyzetes közepe. \[ x=\sqrt{\frac{a^2+b^2}{2}} \notag \]
Előző Fejezet
Vissza: Fejezet
Következő Fejezet

Most kedvező áron az előkészítő csomag

2023 iFeladatok I.

Interaktív feladatok felvételire és emelt szintű érettségire
4.590 Ft 2022/23 tanévre
  • 20 iFeladat automatikus javítással
  • 19 témakör
  • 121 megoldási lépés
  • Megoldássegítő felépítés
  • 2,15 átlagos nehézség (1-3 skálán)
  • A tananyag 2023. június 30-ig érhető el
Előfizetés részletei

2023 Emelt szintű
matematika előkészítő

Kidolgozott feladatok felvételire és emelt szintű érettségire
59.900 Ft 2022/23 tanévre
  • 25 kidolgozott témakör
  • Több mint 200 kidolgozott példa
  • 13 interaktív feladatsor
  • 21 elméleti összefoglaló
  • Felkészülés folyamatos követése, naplózása
  • 2024-től érvényes követelményekkel kiegészítve
  • 25 szóbeli tétel - teljes tételsor
  • A tananyag 2023. június 30-ig érhető el
Előfizetés részletei

2023 Középszintű matematika kurzusok

Tananyag középszintű matematika felkészüléshez
1.750 Ft 2022/23 tanévre, kurzusonként
  • Témakörönkénti előfizetés
  • Megértést segítő magyarázat
  • Definíciók, tételek
  • Kidolgozott típuspéldák
  • Online feladatok, azonnali javítással
  • Felkészülés folyamatos követése, naplózása
  • 2024-től érvényes követelmények alapján
  • A tananyag 2023. június 30-ig érhető el
Előfizetés részletei

Kapcsolat

Dokumentumok

Pénzügyi Partnerünk

CIB Bank

Elfogadott kártyák

Bankkártyák

    Írj nekünk!



    Facebook Map-marker-alt Tiktok

    Ügyfélszolgálat

    • Telefon: +36 30 427-6190
    • hétfő-péntek: 8:00-16:00

    Vásárlási kisokos

      Copyright © iMatek 2020-2025 – Minden jog fenntartva