Mielőtt megvizsgáljuk, hogy hogyan lehet sejtautomatával modellezni a forgalmat, nézzük át röviden, hogy mik is a sejtautomaták. Egy végtelen négyzetrács minden négyzetében élhet egy sejt. Egy sejt állapota véges sok értéket vehet fel, a legegyszerűbb esetben \(\{1,0\}\). A sejtek állapota lépésenként változik oly módon, hogy egy adott sejt állapota a következő lépésben önmaga és szomszédai állapotától függ. A szabályt, amely leírja, hogy egy sejt egy adott állapotból milyen állapotba kerül, átmenetfüggvénynek nevezzük.
A fentiek alapján az egymás fölé rajzolt generációknál egy új négyzet értékét a felette lévő három (balra egy, felette és jobbra egy) cella értéke alapján határozzuk meg. Minden cella két értéket vehet fel, és három cella határozza meg az új generációs négyzet értékét, így összesen \(2^3=8\) féle állapotot definiálunk. Nézzünk egy példát.
A nyolc féle állapot kimeneti értékét tetszőlegesen definiálhatjuk, így összesen \(2^8=256\) szabályrendszert tudunk felállítani az elemi sejtautomaták esetén. (A fenti a \(71=01000111_2\)-es szabály, amely a fehér=0 és fekete=1, kettes számrendszerben felírt számból származik.)
Tekintsünk egy példát. Az új generáció első elemét, amelyet a második sorban sárgával jelöltünk, a felette lévő sorból a szintén sárgával jelölt sejtek, határozzák meg. A fenti \(71\)-es szabályrendszer \(3.\) eleme alapján fehér lesz az eredmény. Az \(5.\) fekete elemet a bordóval keretezett elemekből tudjuk meghatározni, a szabályrendszer \(6.\) tagja alapján.
A bevezetőben megismertük az elemi sejtautomaták működési elvét és láthattuk, hogy miért éppen \(256\) szabályrendszert használunk. A 256 szabály négy csoportba osztható, aszerint, hogy tetszőleges kiinduló állapotból hogyan viselkedik több generáció után.
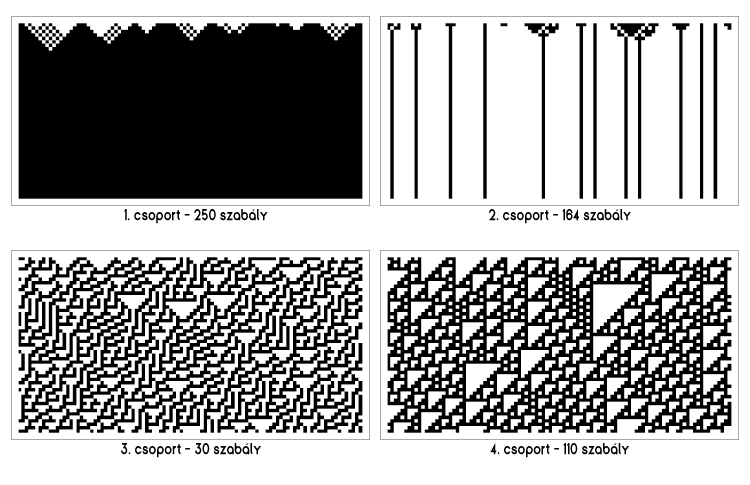
A képeken egy-egy példát láthatunk az osztályokra.
Néhány szabály kiemelt szerepet tölt be. Vizsgáljuk meg közelebbről a \(30\)-as, \(90\)-es, \(110\)-es és \(184\) es szabályokat. A \(30\)-as szabály kaotikus viselkedése miatt véletlenszám generátorként használható. A \(110\)-es szabály alapján működő elemi sejtautomata a 4. csoportba tartozik komplex viselkedése miatt, és a Conway-féle életjátékot adja. A \(110\)-es szabály nem teljesen véletlenszerű, de nem is tartalmaz ismétlődő motívumokat.
\(55\%\)-os telítettség esetén, viszonylag hamar, kb. 600 lépés után minden autó dugóba került és megszűnik a mozgás (a szimuláció \(601.\) képkockája).
A legtöbb érdekességet hordozó átmeneti állapotot, esetünkben \(36\%\)-os telítettség mellett figyelhettük meg, amelyhez \(4000\) lépést modelleztünk (az utolsó \(500\) képkocka látható animálva).
A Biham-Middleton-Levine modell egyszerű feltételezés alapul, amelyet még úgy is heréz általánosítani és gyakorlati alkalmazását tekinteni, ha egy nagyváros úthálózatán próbáljuk meg értelmezni. A modell alapfeltevései túl egyszerűek ahhoz, hogy gyakorlati problémára megoldást kínáljanak, azaz lesz dugó, ha sok az autó. A sejtautomata szabálya lényegében azt mondja, hogy csak egy lépésre gondolkodik előre, és megáll ha vannak előtte, függetlenül attól, hogy egyébként mennyire akadályozza a többieket. Ez nem csak ahhoz a kellemetlen helyzethez vezet nagy autó sűrűség esetén, hogy megáll a forgalom, hanem ahhoz is, hogy nem is lehet tovább indítani az adott szabályrendszerrel. Érdekes továbbfejlesztése lehet a modellnek, ha a mozgó részecskék több eseményt vesznek számításba, esetleg nagyobb távolságból is vesznek adatot, megtanulnak “udvariasan” viselkedni, vagy elsőbbséget adni. A modell mindenképpen továbbfejleszthető, ha a sejtautomata szabályrendszerébe olyanokat kódolunk, hogy pl. a piros autónak elsőbbsége van vagy ha találkoznak, és mindkettő megáll, akkor valamelyik visszalép egy mezőt, ha az üres, esetleg van mód manőverezésre, és megállás esetén a kijelölt iránytól eltérhetnek, és más irányba folytathatják útjukat, persze ha az szabad.
Egy-egy út vagy úthálózat közlekedési sajátosságait figyelembe véve alkothatunk meg olyan szabályokat, amelyek többé kevésbé állandóak és eredményük a gyakorlatba is átültethetők. A Biham-Middleton-Levine modell alapján egy primitív következtetést vonhatunk le: ne engedjünk a forgalomba \(35\%\)-nál több autót, különben végérvényesen dugóba kerülnek. Ebből is látszik, hogy a modell finomítására, komplexebb szabályrendszerre van szükség. Egy körültekintően elemzett közlekedési helyzet, a jól megválasztott (sejtautomata) modellel olyan eredményeket is produkálhat, amely a végeláthatatlan várakozás helyett például az ajánlott sebességről tájékoztatja az autópályán haladókat, annak érdekében, hogy ne alakuljon ki álló kocsioszlop. Ez fontos célja lehet a forgalomszervezésnek, ugyanis az álló kocsioszlop nem csak kellemetlen a benne ülőknek, de az óvatlan vezetők számára balesetveszélyes is.
Copyright © iMatek 2020-2025 – Minden jog fenntartva
