Most már fel tudjuk írni azokat az összefüggéseket, amelyek a korlátokat, peremfeltételeket jelentik, illetve a célfüggvényt is.
\[
\begin{aligned}
2B+A&\leq 44\quad (1.)\\
B+3A&\leq 44\quad (2.)\\
10B+8A&=P\quad (3.)\\
\end{aligned}\notag
\]
Nézzük meg az \((1.)\) egyenlőtlenség jelentését. \(44\) db 1-es típusú alkatrészünk van raktáron, amely felhasználását összesítjük, azaz minden \(A\) termékhez felhasználunk \(1\)-et és minden \(B\) termékhez \(2\)-t belőle. A \((2.)\) egyenlőtlenség hasonlóan értelmezhető. A \((3.)\) egyenlet pedig a profitot mutatja, azaz 8.000 forintot keres a cég az \(A\) termék, és \(10.000\) forintot a \(B\) termék eladásával. A célunk, hogy ezt maximalizáljuk. Az első két egyenletben azért van egyenlőtlenség jel, mert a feltételek alapján minden gyártási párosítás megfelelő, amely maximum 44 alkatrészt használ fel. A profitot nem ismerjük, csak azt, hogy milyen arányban járul hozzá a két termék. Átrendezzük az egyenlőtlenségeket és ábrázoljuk őket.
\[
\begin{aligned}
2B&\leq -A+44\quad \text{kék terület}\\
B&\leq -3A+44\quad \text{piros terület}\\
B&=-\frac{8}{10}A+\frac{P}{10}\quad \text{piros vonal}\\
\end{aligned}\notag
\]
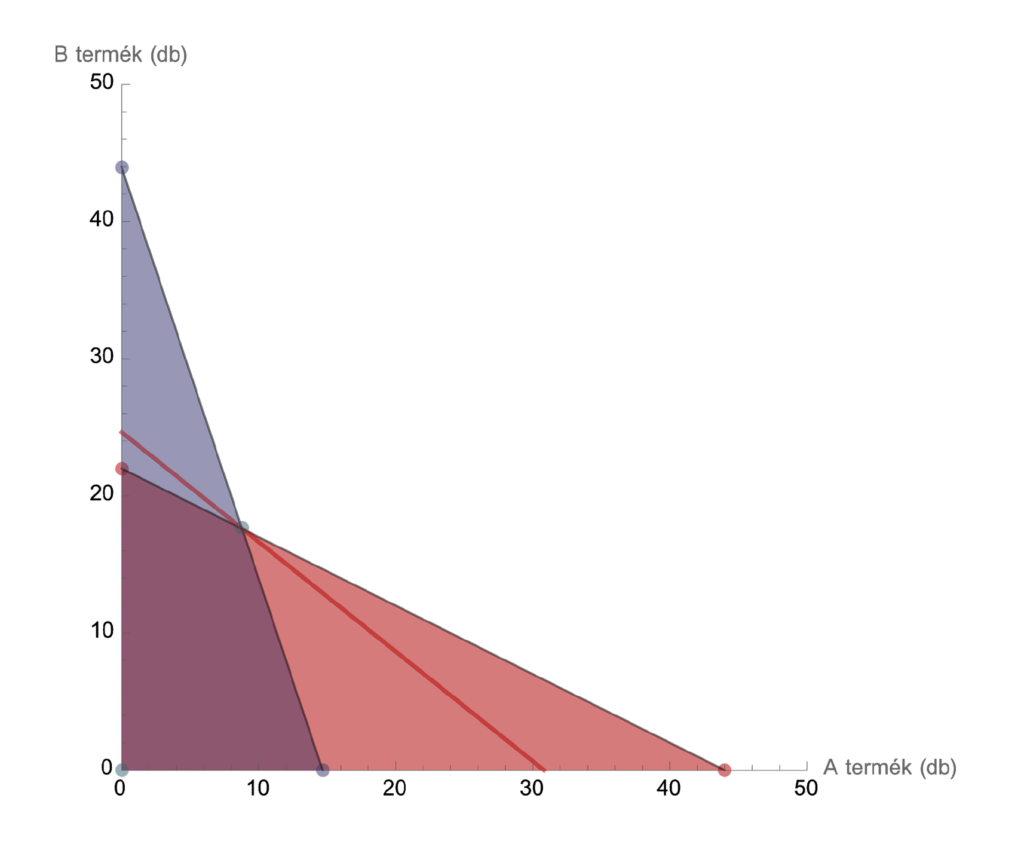
A kék és piros háromszögek közös lila része mutatja azon pontok halmazát, amely mindkét peremfeltételt, a két termék gyártása során a teljes alkatrészigényt figyelembe veszi, azaz a két termékből az ilyen mennyiségű gyártás együttesen megvalósítható a raktárkészletből. A piros vonal helyzetét tekintve egy kicsit már előre szaladtunk. Jelenleg csak annyit tudunk, hogy ezzel a vonallal párhuzamos, ugyanis meredekségét meghatározza az egyes termékeken elérhető profit hányadosa.
Azt könnyen beláthatjuk, hogy minél magasabban van a profit vonal, annál nagyobb összeget jelképez, ugyanis az összprofitot az \(y\) tengellyel vett metszéspontjának második koordinátája adja. Ezt a vonalat úgy szeretnénk megrajzolni, hogy a lehető legmagasabban húzzuk meg, hogy még érintse (vagy áthaladjon) a lila mezőn. Esetünkben a lila mező és a piros vonal közös pontja nem egész koordinátájú \((8,8;\,17,6)\), amely darabáru esetén csak úgy értelmezhető, hogy egy alacsonyabban lévő profit vonalat kell vizsgálnunk, amely áthalad a lila mezőn. Az egyszerűség kedvéért tekintsük most a termékeket ömlesztett árunak, például előkevert betonnak. Ebben az esetben a kapott \((8,8;\,17,6)\) csúcspont meghatározza az optimális mennyiséget, a gyártandó termékekből, hogy a profit maximális legyen, amelyet most már ki is tudunk számolni, \(P=246,4\) eFt.
Természetesen figyelembe vehetnénk több alapanyagot is a gyártás során, amelyek további peremfeltételeket határoznának meg, ezzel bővítve a színes területek számát. Gyakran a megvalósítható tartomány egy sokszög, amelyhez ha ábrázoljuk a profit egyenesét, akkor azt addig kell eltolni, hogy az csak érintse a sokszöget (ez jelenti a maximumot). Könnyű belátni, hogy előfordulhat olyan eset, amikor a profit egyenese nem egy csúcsra, hanem egy oldalra illeszkedik. Ilyenkor nem egyértelmű a megoldás, végtelen sok optimális hely van. Ezek között közömbös a választás a megadott feltételek és célfüggvény mellett.
Előfordul, hogy a profit helyett a költségeket vizsgáljuk. Ekkor minden megfordul, nem az egyenesek alatti, hanem a feletti területeket tekintjük megvalósítható tartománynak, és a költség egyenesét a lehető legalacsonyabb helyzetbe szeretnénk mozgatni, hogy értéke minimális legyen (a lehető legalacsonyabb helyen metssze az \(y\) tengelyt).

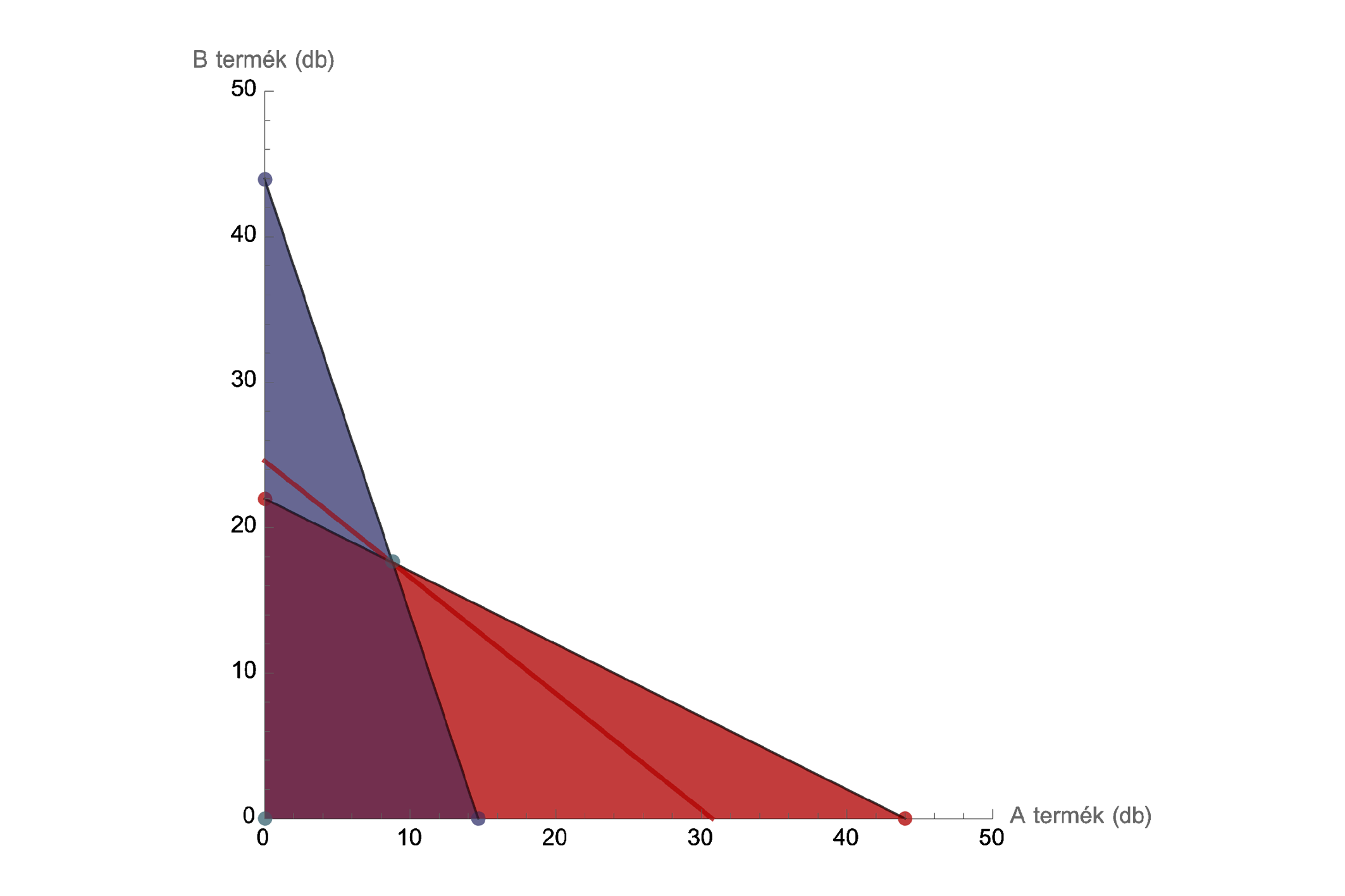

 A kék és piros háromszögek közös lila része mutatja azon pontok halmazát, amely mindkét peremfeltételt, a két termék gyártása során a teljes alkatrészigényt figyelembe veszi, azaz a két termékből az ilyen mennyiségű gyártás együttesen megvalósítható a raktárkészletből. A piros vonal helyzetét tekintve egy kicsit már előre szaladtunk. Jelenleg csak annyit tudunk, hogy ezzel a vonallal párhuzamos, ugyanis meredekségét meghatározza az egyes termékeken elérhető profit hányadosa.
A kék és piros háromszögek közös lila része mutatja azon pontok halmazát, amely mindkét peremfeltételt, a két termék gyártása során a teljes alkatrészigényt figyelembe veszi, azaz a két termékből az ilyen mennyiségű gyártás együttesen megvalósítható a raktárkészletből. A piros vonal helyzetét tekintve egy kicsit már előre szaladtunk. Jelenleg csak annyit tudunk, hogy ezzel a vonallal párhuzamos, ugyanis meredekségét meghatározza az egyes termékeken elérhető profit hányadosa.

 Copyright © iMatek 2020-2024 – Minden jog fenntartva
Copyright © iMatek 2020-2024 – Minden jog fenntartva